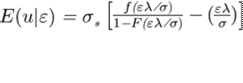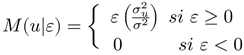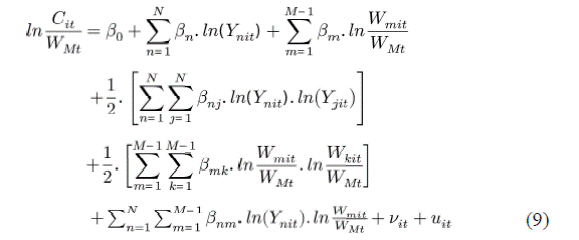Revista de Economía y Estadística | Vol. LIX | N° 1 | 2021 | pp. 37-60 | ISSN 0034-8066 | e-ISSN 2451-7321|
Revista de Economía y Estadística | Vol. LIX | N° 1 | 2021 | pp. 37-60 | ISSN 0034-8066 | e-ISSN 2451-7321|
Instituto de Economía y Finanzas | Facultad de Ciencias Económicas |
Universidad Nacional de Córdoba
http://www.revistas.unc.edu.ar/index.php/REyE
 Esta obra está bajo una Licencia Creative Commons
Atribución-No Comercial-Sin Derivar 4.0 Internacional
Esta obra está bajo una Licencia Creative Commons
Atribución-No Comercial-Sin Derivar 4.0 Internacional
Consideraciones metodológicas acerca del Análisis Estocástico de Frontera en modelos de datos de panel:
evidencias del modelo ECF orientado a costos en el Sector Bancario Argentino
Methodological considerations upon Stochastic Frontier Analysis for panel data models: evidence
from cost-efficiency ECF model in the Argentine Banking Sector
Ignacio G. Girela
Universidad Nacional del Córdoba, Facultad de Ciencias Económicas (Córdoba, Argentina)
ignacio.girela@unc.edu.ar
José M. Vargas
Universidad Nacional del Córdoba, Facultad de Ciencias Económicas (Córdoba, Argentina)
jose.vargas@unc.edu.ar
Resumen
En este artículo analizamos metodológicamente el desempeño del modelo de datos de panel Error Components Frontier
(ECF) basado en el método
de Análisis de Frontera Estocástica (SFA) para estudios de eficiencia
relativa orientado a costos ante la disponibilidad de paneles pequeños y con presencia de valores atípicos. Mediante
una serie de simulaciones y una posterior
aplicación al sector bancario argentino para el período
2005- 2014, mostramos que bajo
estas condiciones un modelo SFA puede no ser
adecuado para hacer un análisis
de eficiencia relativa. Estos resultados son relevantes para la literatura
empírica ya que los paneles pequeños con presencia
de valores atípicos representan escenarios típicos de los sectores económicos de economías en desarrollo.
Palabras clave: datos de panel; SFA; eficiencia orientada a costos; entidades bancarias; benchmarking; simulaciones.
Códigos JEL: C14, C33, D24, G21, L51.
Fecha de recepción: 03/12/2019. Fecha de aceptación: 28/06/2021
Abstract
In this paper we make a
methodological analysis of the Error Components Frontier (ECF) panel data model performance based on Stochastic Frontier Analysis (SFA)
method for cost efficiency
benchmarking in the presence of
small panels and outliers. By means of a set of simulations and a subsequent application to the Argentine
banking sector during the period 2005-2014,
we prove that under these conditions an SFA model may not be adequate for benchmarking. These results
are relevant for the empirical literature since small panels with the presence
of outliers represent classical scenarios in developing economies
industries.
Keywords: panel data; SFA; cost efficiency; banking entities;
benchmarking; simulations.
JEL Code:
C14, C33, D24, G21, L51.
I. Introducción
Los estudios de eficiencia relativa o benchmarking tienen por
objetivo proveer información acerca del desempeño de una firma en comparación de otras. Esto implica estimar los niveles
de eficiencia de las firmas de un sector
económico y establecer un ranking que permita realizar un análisis comparativo. Aunque existen diversos
métodos paramétricos, no paramétricos y semi-paramétricos orientados a la
medición de eficiencia de las firmas, todos coinciden
en la utilización de los datos de las firmas
que pertenecen a un sector económico para estimar una
frontera de eficiencia a partir de la cual
se evalúa el desempeño de éstas. Dentro de una industria competitiva, esta clase de estudios resultan relevantes
ya que proporcionan información valiosa
para la toma de decisiones de directores ejecutivos o hacedores de política
(Berger & Humphrey,
1997).
Considerando que uno de los principales intereses de las firmas es la minimización de costos, una parte del benchmarking se
ha dedicado a estudiar la eficiencia orientada a costos. Los dos
métodos más utilizados en la literatura son el DEA (Data Envelopment
Analysis) y SFA (Stochastic Frontier Analysis).
El primero es un enfoque no paramétrico que estima una frontera desconocida y computa medidas
de eficiencia a través de
programación matemática mientras que
el segundo es un método paramétrico que utiliza técnicas econométricas para realizar
el benchmarking (Bogetoft &
Otto, 2010).
Siguiendo a Lovell (2003), “ningún método es estrictamente
superior al otro”. Esto es porque
cada uno presenta ventajas y desventajas. Por ejemplo, al ser un modelo econométrico, SFA considera los errores
aleatorios en el problema de optimización
mientras que DEA puede estar afectado por una componente aleatoria no medible (Coelli, et al.,
2005). Sin embargo, en SFA se debe realizar supuestos acerca de la
forma funcional de la frontera de eficiencia a estimar. En este sentido,
DEA resulta más flexible ya que no requiere supuestos acerca de la forma de la frontera
(Bauer, et al.,
1998). De hecho, a fines de conservar
algunas ventajas y atenuar desventajas de cada enfoque, han surgido métodos SFA semiparamétricos (entre
ellos Henningsen & Khumbakar, 2009; Vidoli, F., & Ferrara, G. 2015;
Ferrara, G., & Vidoli, F. 2017) e
incluso no-paramétricos en el marco de SFA (Kumbhakar, et. al., 2007)
Por otro lado, no sólo es de interés estimar una frontera
de eficiencia y hacer un análisis comparativo de las
firmas sino también estudiar comportamiento y los determinantes del desempeño de
las firmas en el tiempo. De este modo,
los métodos de eficiencia relativa se han extendido para datos de panel. Esto ha sido ampliamente estudiado
en SFA y más recientemente para DEA (Surroca, et al., 2016).
En resumen, ha habido numerosos avances para mejorar los
distintos enfoques mitigando
sus desventajas e incorporar las ventajas que otorga, en términos de inferencia, un modelo de datos de panel. No obstante, a pe sar de estos avances, no existe un
escenario ideal, es decir, un modelo de benchmarking
que sea estrictamente superior a todos. Por
esta razón, en la literatura empírica
se tiende a optar por uno u otro modelo dependiendo qué aspectos de la eficiencia se desean destacar.
En lo que concierne a estudiar la eficiencia utilizando datos de panel con el objetivo de analizar la tendencia
de la eficiencia media en costos en el tiempo, el modelo Error Components Frontier (ECF) propuesto por Battese & Coelli (1992) es de los más
utilizados en la literatura empírica (Kumbhakar, et al., 2014). El ECF
es un modelo paramétrico bajo el enfoque SFA
con la ventaja de incorporar al tiempo como una variable
explicativa.
Sin embargo, pese a ser ampliamente utilizado en la literatura empírica, poco se
ha estudiado sobre el ajuste
del modelo ante la presencia de valores atípicos dentro del panel. En especial, en paneles
relativamente pequeños (con pocos
cortes transversales). Esto resulta relevante ya que las economías de países de ingresos
medios o bajos,
no presentan un alto nivel
de competencia en sus industrias ya sea por posiciones oligopólicas o
mercados no lo suficientemente grandes
para aprovechar economías
de escala. En este sentido, el presente trabajo tiene dos objetivos: por un lado, obtener un conjunto de lineamientos metodológicos para aplicar un modelo SFA para
datos de panel tan ampliamente utilizado como el ECF considerando la presencia de outliers en paneles
con pocos cortes transversales y por el otro,
aplicar el modelo ECF orientado a costos para el caso del sector
bancario argentino para el período
2005-2014, para el cual no encontramos razones
para pensar en la existencia de una componente de ineficiencia
concluyendo que la convergencia del modelo proviene de la influencia de valores atípicos. Este estudio
aplicado resulta interesante porque la industria
bancaria y financiera son
sectores económicos que suelen presentar valores atípicos (Berger & Humphrey, 1991) y, además,
es un panel relativamente pequeño (aproximadamente 50 bancos) en comparación con otras
aplicaciones del modelo SFA en el sector bancario[1]
El trabajo se estructura como sigue: en la segunda sección se presentan
los fundamentos y una breve revisión de la literatura sobre el método SFA para datos de panel orientado a
costos. En la tercera sección, se describe el
modelo ECF y los métodos de estimación. Cuarto, se llevan a cabo una serie de simulaciones para evaluar el ajuste del modelo ECF ante la presencia de outliers. En la quinta sección
se aplica el modelo ECF al sector bancario argentino
para el período 2005-2014 y se evalúa la performance del modelo en base
a los resultados de la cuarta sección. Finalmente, concluimos con un conjunto de estrategias metodológicas
para realizar un SFA utilizando el modelo ECF y futuras líneas de investigación.
II.
Método SFA orientado a costos para datos de panel: una revisión de la literatura
El método SFA provino de la frontera de función de
producción estocástica inicialmente propuesta por Aigner, et al. (1977)
y Meeusen & van den Broeck (1977) en la cual se incluye
explícitamente la ineficiencia a través
de un error compuesto: ϵ=ν+u, donde ν es el término de error normal y u es un término no negativo
que representa la ineficiencia.
Aunque en su origen el enfoque SFA estaba orientado a
estimar una frontera de producción,
siguiendo a Schmidt & Lovell
(1979) y Coelli, et al. (2005), a partir de simples cambios
de signo, las técnicas de estimación de los parámetros de la frontera de
producción pueden aplicarse del mismo modo
para la función de costos. En otras palabras, la frontera de eficiencia en el caso orientado a costos se basa en la estimación de una
función de costos para todo el sector económico bajo análisis.
Un modelo SFA orientado a costos para datos de panel se
define formalmente de la siguiente
manera:
ln(Cit)= X'it β + εit (1)
donde ln(Cit) es el logaritmo del costo de la i-ésima firma en el
t-ésimo período de observación para i=1,…,N y t=1,2,…,T.;
X'it es el vector
de outputs y precio de los inputs para la i-ésima firma en el t-ésimo período
de observación;
β es el vector columna de parámetros desconocidos de la función
de costos a estimar;
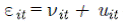 es el
término de error compuesto;
es el
término de error compuesto;
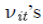 se asumen que son errores
aleatorios independientes e idénticamente distribuidos
se asumen que son errores
aleatorios independientes e idénticamente distribuidos 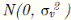 Es decir,
Es decir, 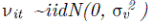
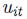 ’s son variables no negativas que representan la ineficiencia. Se asume que tiene una distribución asimétrica.
’s son variables no negativas que representan la ineficiencia. Se asume que tiene una distribución asimétrica.
Por otra parte, la eficiencia en costos de la
i-ésima firma se define como el cociente entre el costo mínimo y el costo observado de
la i-ésima firma (Coelli, et al. (2005).
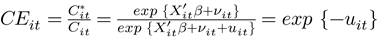 (2)
(2)
donde Cit es el costo
observado de la i-ésima firma y Cit
* es el costo
mínimo. La medida
de eficiencia en costos (ecuación
2) toma valores
entre 0 y 1, mientras más
cercano a 1, más eficiente. En base a la ecuación (2), notamos que el problema en la estimación de la frontera de
eficiencia para datos de panel
consiste en proponer un método de estimación de uit para
cada firma i en cada momento
t.
Originalmente, el método SFA fue propuesto para datos transversales. Los primeros modelos
SFA para datos de panel
fueron propuestos por Pitt
& Lee (1981), Schmidt & Sickles (1984) y Battese & Coelli (1988).
El segundo asume que los términos de ineficiencia u son parámetros fijos por lo que no son necesarios supuestos acerca de su distribución. En cambio, los dos
modelos restantes asumen que u
es una variable
aleatoria y tiene una
distribución asimétrica half-normal o normal truncada. No obstante, los primeros
modelos SFA para datos de panel presuponen que la ineficiencia es invariante en el tiempo lo cual representa un supuesto muy restrictivo.
 Cornwell, et. al.
(1990) desarrollaron el primer
modelo SFA en el cual la eficiencia
varía en el tiempo utilizando métodos tradicionales de da- tos de panel para estimar la frontera,
pero con la desventaja de agregar una gran cantidad
de parámetros. Lee & Schmidt
(1993) también especificaron un modelo donde la eficiencia varía en el tiempo con menor
cantidad de parámetros a estimar que
el anterior. Sin embargo, supone que el patrón
temporal de uit es igual para todas
las firmas.
Cornwell, et. al.
(1990) desarrollaron el primer
modelo SFA en el cual la eficiencia
varía en el tiempo utilizando métodos tradicionales de da- tos de panel para estimar la frontera,
pero con la desventaja de agregar una gran cantidad
de parámetros. Lee & Schmidt
(1993) también especificaron un modelo donde la eficiencia varía en el tiempo con menor
cantidad de parámetros a estimar que
el anterior. Sin embargo, supone que el patrón
temporal de uit es igual para todas
las firmas.
Battese & Coelli (1992) propusieron el modelo Error Components Frontier
(ECF), generalizando el modelo de Kumbhakar (1990). La novedad de este modelo es que cuenta con la posibilidad de utilizar datos de panel no balanceados, donde el tiempo varía y es una variable
explicativa permitiendo evaluar
la tendencia de eficiencia media del sector
a lo largo del tiempo.
Además, la ventaja de la estructura de este modelo es que el parámetro
de la variable explicativa tiempo es más fácil de interpretar que los demás modelos donde el tiempo varía.
Battese & Coelli (1995) plantearon un modelo SFA para
datos de panel denominado Efficiency Effects
Frontier (EEF) que determina cuáles son los factores exógenos que
influyen sobre la eficiencia. No obstante, no
permite realizar inferencias
acerca del comportamiento de la ineficiencia
en el tiempo.
En la literatura se ha destacado que los modelos SFA para datos de panel donde el tiempo varía asumen que el
intercepto es igual para todas las firmas.
Greene (2005a, b) introdujo un modelo para datos de panel donde el intercepto es específico al corte
trasversal y los parámetros se estiman por Efectos
Fijos o Efectos Aleatorios (a estos modelos se los denominó “True Fixed Effects – TFE” y “True Random
Effects – TRE”). La estructura del modelo
de Greene (2005a, b) logra separar el efecto del tiempo sobre la ineficiencia y el efecto no observado de cada firma. No obstante, el efecto no observado de cada firma añade un componente de heterogeneidad, pero no forma parte de la ineficiencia lo cual arroja ciertas interrogantes acerca de si debe incluirse
o no y cuáles son las ventajas
de ello.
Estos no son los únicos modelos SFA para datos de panel.
Existen otros avances que en general abordar
problemas particulares de algunos modelos. Por ejemplo, los supuestos sobre
la distribución de u, la forma funcional del
modelo, el método de estimación, entre otros.
Sin embargo, pese a numerosos
desarrollos, no existe un modelo que supere al resto en cualquier aspecto. De hecho, los más utilizados en la literatura
empírica son los modelos de Battese
& Coelli y Greene (Kumbhakar, et. al., 2014). En este sentido, las contribuciones
metodológicas también se orientan a evaluar el
desempeño de los modelos para obtener lineamientos para aplicaciones empíricas
futuras.
En el caso de este trabajo, se pone bajo análisis el modelo
ECF de Battese & Coelli (1992)
que es de los más utilizados cuando
se tiene un panel
desbalanceado y se desean hacer inferencias acerca de la influencia del tiempo sobre
la eficiencia. Por ello, en la siguiente sección se describe
el modelo ECF y su metodología de
estimación. Luego, mediante una
serie de simulaciones veremos que el
modelo no es robusto ante la presencia de outliers para paneles con pocos individuos en el caso donde el tiempo varía
y se puede analizar la tendencia de la eficiencia media en el tiempo
(contribución principal del modelo). Posteriormente, aplicaremos el modelo al
sector bancario argentino para el período 2005-2014. Éste representa un caso interesante para evaluar el ajuste del modelo ECF por dos razones: primero, se han aplicado modelos SFA de
datos de panel en este sector sin hacer consideraciones sobre si el modelo
estima correctamente (Ferro, et al., 2013); segundo, como se mencionó en la primera sección, la industria
bancaria y financiera son sectores económicos que suelen presentar
valores atípicos (Berger
& Humphrey, 1991) lo cual no puede quedar fuera del análisis.
III. Modelo
ECF: Metodología y Estimación
Como bien comentamos en las secciones anteriores, ECF es un modelo SFA
para datos de panel donde el tiempo varía. Es decir, el tiempo es una variable explicativa y es posible
inferir si la eficiencia media en el sector no varía, disminuye o aumenta en el tiempo.
La estructura general del modelo es la misma descrita en la
ecuación (1). Por otra parte, el modo en que define el término de ineficiencia u es de la siguiente forma:
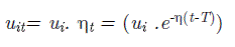
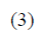
donde i=1,…,N y t=1,…,T y uit es una variable
no negativa.
La eficiencia en costos continúa definiéndose del
mismo modo que la ecuación (2). El modelo es tal que el
término uit, decrece, permanece constante
o incrementa a medida que t
aumenta,
si η>0, η=0 o η<0,
respectivamente. En caso de que η¹0, el tiempo es una variable significativa. En otras
palabras, de acuerdo con el modelo
ECF, la eficiencia en costos debe incrementarse para todo el sector
cuando la tasa relativa es positiva (η>0), decrecer
cuando la tasa relativa es negativa (η<0), o bien, permanecer constate (η=0) (Figura 1).
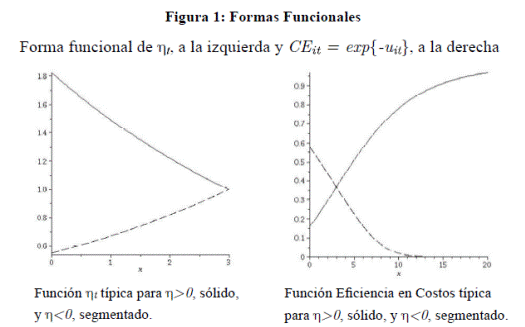
La ecuación (3) es una forma sencilla de introducir el tiempo de manera
que se puedan obtener conclusiones acerca de su efecto sobre la ineficiencia. En el trabajo de Lee & Schmidt (1993) el término uit se define:
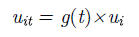
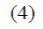
donde g(t) son variables dummies del tiempo.
Este modelo no asume una forma
paramétrica al introducir el tiempo lo cual provoca que los patrones de ineficiencia sean excesivamente variables
(Han, et. al., 2005).
Kumbhakar (1990) utiliza la siguiente función paramétrica
para introducir a la variable tiempo:
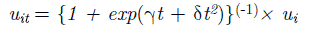
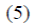
De este modo, la ecuación (3) es una generalización de la ecuación (5) donde se estima sólo un parámetro adicional
(η) que resulta más fácil de interpretar que los dos parámetros de la ecuación (5).
Un
paso importante a la hora de llevar a cabo un modelo SFA es definir
el supuesto de distribución de la variable
u. Al ser no negativa, los supuestos acerca de su distribución deben estar en función
de distribuciones asimétricas. A
saber, una distribución half-normal con un parámetro de escala 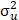 , es decir, uit ~ iidN+ (0,
, es decir, uit ~ iidN+ (0, 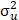 ). Otros
supuestos válidos de distribución son una
normal truncada (uit~iidN+ (μ,
). Otros
supuestos válidos de distribución son una
normal truncada (uit~iidN+ (μ, 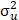 )), una distribución exponencial con
media λ (uit ~iidG(λ,0)), o bien, una gamma con media λ y m grados de libertad (uit ~ iidG(λ,m)). Estos
supuestos en los modelos paramétricos resultan
esenciales para separar la componente de ineficiencia u del ruido estadístico ν (Jondrow, et. al,
1982). Nótese que las estimaciones de la ecuación (2) serán distintas según el
supuesto de distribución que tomemos. No obstante,
los resultados en cuanto al ranking de eficiencia son generalmente robustos
a las distribuciones (Coelli, et. al., 2005).
)), una distribución exponencial con
media λ (uit ~iidG(λ,0)), o bien, una gamma con media λ y m grados de libertad (uit ~ iidG(λ,m)). Estos
supuestos en los modelos paramétricos resultan
esenciales para separar la componente de ineficiencia u del ruido estadístico ν (Jondrow, et. al,
1982). Nótese que las estimaciones de la ecuación (2) serán distintas según el
supuesto de distribución que tomemos. No obstante,
los resultados en cuanto al ranking de eficiencia son generalmente robustos
a las distribuciones (Coelli, et. al., 2005).
La estimación de los parámetros del modelo se realiza mediante
máxima verosimilitud (ML). Debido a que la función verosimilitud es no lineal
con respecto a los
parámetros, es necesaria la siguiente reparametrización γ≡ (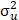 )/σ y σ ≡
)/σ y σ ≡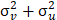 (Battese &Corra,
1977), Nótese que γ∈ [0,1] y, siguiendo su
definición, otorga información acerca de en qué proporción los desvíos de la
frontera se deben a la ineficiencia, i. e., si γ
es un valor cercano a
1, los desvíos de la frontera se deben casi totalmente a la ineficiencia y si γ
es cercano a cero, entonces no debería existir ineficiencia significativa.
(Battese &Corra,
1977), Nótese que γ∈ [0,1] y, siguiendo su
definición, otorga información acerca de en qué proporción los desvíos de la
frontera se deben a la ineficiencia, i. e., si γ
es un valor cercano a
1, los desvíos de la frontera se deben casi totalmente a la ineficiencia y si γ
es cercano a cero, entonces no debería existir ineficiencia significativa.
Como hemos anticipado anteriormente, el método paramétrico
SFA implica estimar la componente de
la ineficiencia u para luego obtener el nivel de
eficiencia (ecuación 2). Para modelos de datos de panel, Jondrow, et. al., (1982) proponen estimadores del término u los
cuales son utilizados en los mencionados modelos
de Battese & Coelli y Greene (Bellotti,
et al., 2013).
Los estimadores de Jondrow, et. al. (1982) toman la esperanza
condicionada de u dado el error compuesto ε. Prueban que tal esperanza condicionada es una normal truncada en cero
para los casos donde se supone que el
término u tiene distribución half-normal y exponencial. En particular, la esperanza
de u dado ε de acuerdo con las ecuaciones (6) y (7).
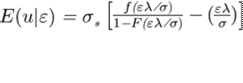 (6)
(6)
para el caso half-normal, donde 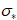 =
= 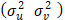 / s2,
/ s2, 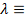 [(
[( 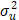 /
/ 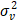 )]-0,5, ¦
y F son la
función de densidad y función de distribución acumulada de la normal respectivamente.
)]-0,5, ¦
y F son la
función de densidad y función de distribución acumulada de la normal respectivamente.
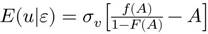 (7)
(7)
para el caso exponencial, donde 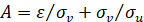
Sin embargo, el estimador más robusto es la moda de la distribución de u dado ε para
estimar el término de ineficiencia que tiene la siguiente expresión:
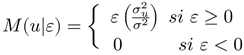 (8)
(8)
No obstante, al estimar por ML, el algoritmo de Newton-Raphson sólo converge si verifica que los residuos de la estimación por mínimos cuadrados ordinarios (OLS) presentan un sesgo a derecha. Este sesgo ha de
inter pretarse como un fenómeno
de ineficiencia captado
en el error compuesto ε (Henningsen, 2018).[2]
IV.
Simulaciones
En primer lugar, para evaluar el desempeño del modelo ECF
en estimar los parámetros ante la presencia de outliers se llevaron a cabo una
serie de simulaciones. En particular, simulamos residuos SFA la siguiente
forma:
●
Sabemos que ε̂ = ν̂ + û ; vit ~ iidN(0, 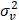 ) y uit ~ iidN+(0,
) y uit ~ iidN+(0, 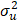 )
)
Entonces, simulamos unos residuos ε̂sim planteando
parámetros 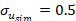 ,
, 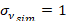 y por lo tanto un
y por lo tanto un 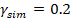 .
.
●
Planteamos
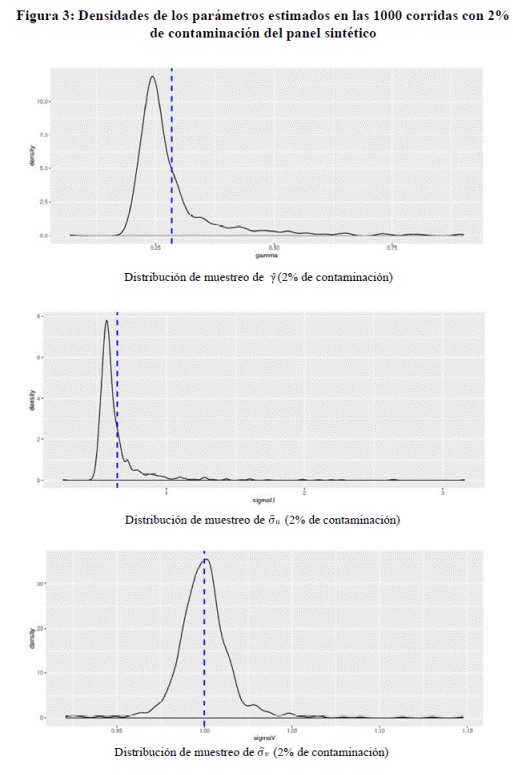
un panel relativamente pequeño: 50 cortes transversales y t=10. En el panel, ordenamos la distribución de 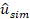 para asegurarnos saber que la eficiencia
aumente del primer al último individuo e incremente en el tiempo.
para asegurarnos saber que la eficiencia
aumente del primer al último individuo e incremente en el tiempo.
●
Estimamos
el modelo ECF 1000 veces (donde los residuos de cada estimación
serán los residuos sintéticos del primer punto). En cada estimación, evaluaremos cómo el modelo
estima los parámetros σv , σu y
●
Para
simular la presencia de outliers y realizar una comparación introducimos una contaminación del 2% de nuestros residuos
(una variable c~N(μ=3, σ2=0.01) sobre las primeras 10
observaciones, i. e, la firma más ineficiente) y estimamos el modelo 1000 veces nuevamente.
De este modo, tenemos las estimaciones
de dos modelos ECF, uno sin contaminación y otro con presencia de valores
atípicos.
En la Figura 2 se muestran las densidades de los parámetros estimados
en las 1000 corridas sin contaminación. Como puede observarse, en ausencia de valores atípicos el modelo ECF
estima correctamente, i. e., la moda
de σv , σu y γ son iguales
a la media (línea vertical punteada) y son iguales
a los valores fijados en la simulación (γ= 0.2, σu = 0.5 y σv =1). Por
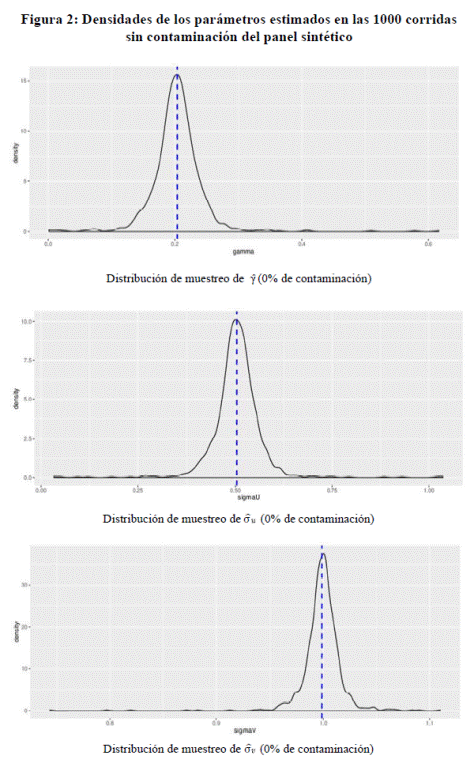
otra parte, la Figura 3, exhibe las densidades de los parámetros
estimados en las 1000 corridas con
una contaminación del 2%. A excepción del parámetro σv, ante la presencia de valores atípicos el método SFA encuentra
dificultades para estimar σu, y por consiguiente, γ. Nótese que existe una mayor sesgo
a derecha en la estimación de estos dos parámetros ya que la media es mayor a la moda (la moda es 0.25 en el caso de
γ ̂ –mayor a 0.2 ̵ y mayor a 0.5 en el caso
de σ̂u ). Nótese que hay casos de
sobreestimaciones excesivamente grandes (el doble e incluso el triple mayor al
verdadero parámetro) En resumen, ante
la presencia de outliers hay una tendencia en el modelo a sobreestimar los parámetros γ y σu.
Otras experimentaciones de la misma simulación con
presencia de outliers sugiere
que a medida que aumenta
el número de cortes transversa- les, a partir de 200, el modelo ECF estima correctamente los
parámetros γ y σu.
V. Modelo ECF aplicado al sector bancario argentino
2005-2014
Como hemos mencionado anteriormente y en base a las conclusiones obtenidas de las simulaciones, para
demostrar el efecto de los valores atípicos en el modelo ECF para paneles
cortos resulta interesante su aplicación al sector bancario porque es un sector
que suele presentar de outliers (Berger &
Humphrey, 1991) y se ha aplicado este mismo modelo en la industria bancaria argentina
sin considerar estos aspectos del sector (Ferro,
et al., 2013).
El primer paso para aplicar el modelo es definir las variables
explicativas y de respuesta. Al tratarse de una función de costos, las
variables independientes son los
outputs y los precios de los inputs y la variable dependiente son los costos
totales de las firmas.[3] Esta información se resume en la Tabla 1.

Los datos corresponden al mes de diciembre de 49 bancos que operaron
ininterrumpidamente en Argentina durante el período 2005-2014. Los datos se obtuvieron de los balances
e informaciones complementarias de las entidades
financieras publicados por el Banco Central de la República Argentina
(BCRA).
Segundo, es necesario definir la forma funcional de la frontera de eficiencia a estimar, en este caso, la
función de costos. En total, se ensayaron cuatro
modelos de costos con distintas variaciones. De todos esos, el modelo presentado es el que mejores residuos OLS
exhibió a los fines de estimar la frontera
de eficiencia mediante el método SFA. Por ello, se asume una forma funcional translogarítmica con imposición de la condición de
homogeneidad lineal que se logra tomando el precio de un input como numerario, la cual adquiere
la siguiente forma:
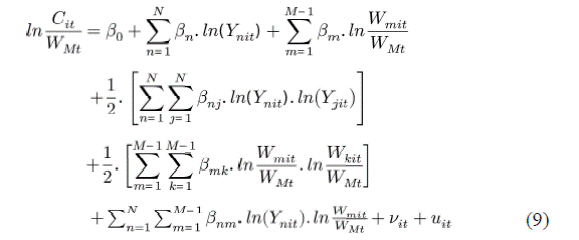
donde Yit y Wit representan los outputs
y los precios de los inputs de la i-ésima firma respectivamente y la parte lineal de la ecuación
corresponde la forma funcional de la Cobb-Douglas linealizada.
Tercero, se debe establecer un supuesto acerca
de la distribución del
término de ineficiencia. Debido a que los uit ’s son no negativos, los supuestos
sobre su distribución deben estar
en función de distribuciones asimétricas como las mencionadas anteriormente. En este caso, se asume una distribución half-normal, es decir, 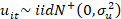 .
.
Cuarto, siguiendo a Henningsen (2018), se debe previamente estimar un modelo OLS con el objetivo de encontrar
un sesgo a derecha en la distribución de los residuos. Ese sesgo ha de interpretarse como un fenómeno de ineficiencia que se capta en un
error compuesto lo cual habilitaría la esti-
mación por un modelo SFA. Si se cumple la condición anterior,
se procede a estimar el modelo ECF por método SFA. Para estimar el modelo se utiliza el paquete frontier de R (Coelli & Henningsen, 2017).
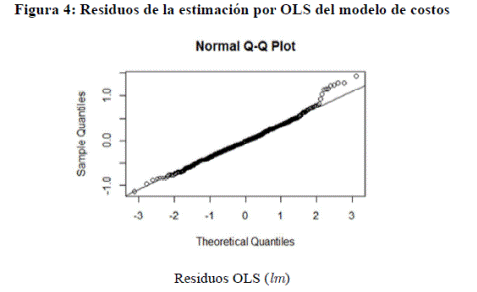
Los residuos de la estimación por OLS exhiben un leve sesgo
a derecha (permitiendo que la estimación del modelo SFA converja). Esto se puede ver en un gráfico QQ-norm en
la Figura 4 donde evidentemente el sesgo a derecha de los residuos OLS se deben a un fenómeno
de outliers.
Sin embargo, como hemos mencionado, el modelo SFA converge
y los parámetros estimados son los
siguientes: γ̂ = 0.97, σ̂u
=1.01 y σ̂v
=0.17 (similar al trabajo de Ferro, et al.
(2013) citado anteriormente). Como γ̂→1, los resultados nos advierten que los
desvíos de la frontera se deben a la ineficiencia.
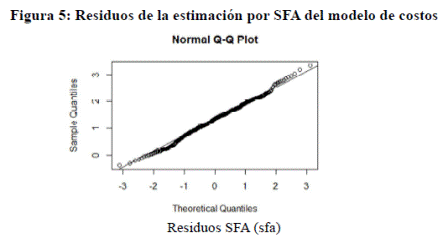
Por lo tanto, es de esperarse un pronunciado sesgo a derecha en la distribución de los residuos SFA lo
cual no es el caso. La Figura 5 muestra la distribución de los residuos
SFA los cuales se distribuyen similar a una normal
con colas más pesadas y su centro de masa corrido hacia la derecha. Estos resultados nos permiten
deducir que el modelo no estima correctamente.
En base a los resultados de las simulaciones, deducimos que el modelo está sobreestimando severamente la componente de ineficiencia (σu)
y por lo tanto el parámetro γ. De
hecho, como podemos ver en la Figura 6, para
los parámetros estimados en el modelo ECF 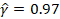
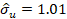 y
y 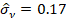 ), el
gráfico QQ-norm de los residuos SFA deberían tener un pronunciado sesgo a la derecha (esto es así porque γ→1) a diferencia
de los resultados obtenidos.
), el
gráfico QQ-norm de los residuos SFA deberían tener un pronunciado sesgo a la derecha (esto es así porque γ→1) a diferencia
de los resultados obtenidos.
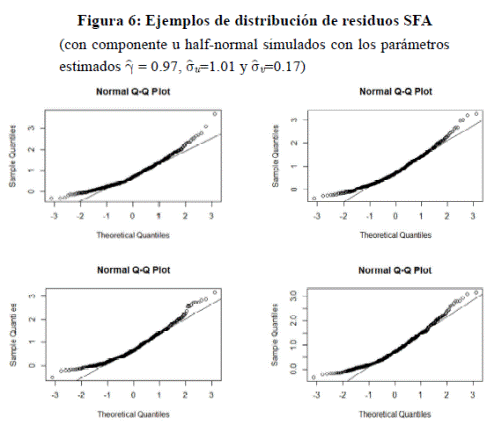
Por lo tanto, el sesgo a derecha de los residuos OLS está provocado por un pequeño conjunto de valores
atípicos permitiendo al modelo ECF converger, pero asimismo sobreestimar los parámetros considerablemente.
Un análisis de los residuos OLS de la Figura 4 muestra que
los valores atípicos pertenecen a varios bancos.
Mediante un análisis
posterior, una eliminación de estos bancos no sólo reduce la influencia de los outliers y el número de cortes transversales sino también que
surgen nuevos valores atípicos para
el nuevo subconjunto de datos repitiendo el mismo problema (sesgo a la derecha de los residuos OLS, convergencia del modelo ECF, pero
sobreestimación severa de la componente de ineficiencia). Procediendo sucesivamente con la eliminación de los
datos atípicos, se repite la misma situación
hasta el punto donde los residuos OLS no muestran el sesgo a de- recha que
permita al modelo ECF converger
develando la alta
sensibilidad del modelo ECF a valores atípicos.
La imposibilidad de estimar un modelo SFA puede deberse a que el conjunto de individuos es tan
pequeño que no existen ineficiencias o bien,
más plausiblemente, no hay diferencias
en términos de eficiencia discernibles estadísticamente.
Por lo tanto, al ser un modelo econométrico, SFA asume que existe una frontera de eficiencia y, aunque el modelo
converja, es posible que ni siquiera
exista una componente de ineficiencia para los datos disponibles.
VI. Conclusiones finales
A través de una serie de simulaciones, hemos demostrado que uno de los modelos SFA para datos de panel
más utilizados en la literatura empírica como el modelo ECF es extremadamente
sensible a la presencia de valores
atípicos cuando el número de cortes transversales en el panel es relativamente pequeño. Los outliers afectan
severamente el análisis ya que provocan
el sesgo a derecha de los residuos OLS permitiendo converger al modelo SFA, pero con estimaciones de los
parámetros sumamente erróneas socavando
el análisis de inferencia. Sólo con paneles relativamente grandes, aproximadamente n=200, el modelo
ECF estima correctamente a pesar de los outliers.
El sector bancario argentino es un caso típico de panel pequeño con presencia de outliers. Una
aplicación del modelo ECF orientado a costos
sobre este sector devela los problemas del modelo bajo estas condiciones.
Estos resultados son relevantes para la literatura empírica por las siguientes razones. Los países poco
industrializados presentan en general bajos
niveles de competencia en sus sectores económicos. En este sentido la presencia de valores atípicos puede
derivarse de la mayor volatilidad de la economía
de estos países, así como la presencia de posiciones oligopólicas puede traducirse en casos de paneles con
pocos cortes transversales como hemos
visto. Por lo tanto, si se ignoran estas condiciones que suelen caracterizar a
los países en vías de desarrollo, podemos realizar un estudio de eficiencia
relativa para tomar decisiones como SFA donde el modelo converja sin que ese hecho sea garantía de que exista una componente de ineficiencia y, de este modo, arrojando
resultados sistemáticamente erróneos tal como
hemos demostrado. Esto es así porque, metodológicamente, SFA asume la existencia de una frontera de eficiencia y,
en particular, este trabajo devela que
bajo ciertas condiciones tal frontera de eficiencia puede no ser discernible estadísticamente, al menos para un modelo ECF orientado
a costos.
En conclusión, para la aplicación de un modelo SFA
orientado a costos destacamos algunos lineamientos metodológicos. Primero, es
recomendable partir de paneles relativamente grandes para mitigar el efecto de
los valores atípicos. Segundo,
siguiendo a Henningsen (2018), una vez elegidas las variables y la forma funcional del modelo, se debe estimar
el modelo por OLS para encontrar un sesgo a derecha en los residuos. Tercero, estudiar si el
sesgo no es consecuencia de outliers. En caso de disponer de un panel pequeño, los outliers afectarán las
conclusiones del análisis. Dentro de
las líneas de investigaciones futuras
incluimos comparar en situaciones similares a las descriptas, paneles pequeños
en presencia de casos atípicos, otros métodos de estimación como DEA.
VII.
Referencias
Aigner, D. J., Lovell, C. A. K. & Schmidt,
P. (1977). Formulation and estimation of stochastic frontier production
function models. Journal of Econometrics,
6(1): 21-37.
Battese, G. E. & Corra,
G. S. (1977). Estimation of a production frontier model: with
application to the Pastoral zone of eastern Australia. Australian
Journal of Agricultural Economics, 21, 169-179.
Battese, G. E., & Coelli, T. J. (1988). Prediction of firm-level
technical efficiencies with a
generalized frontier production function and panel data. Journal of Econometrics, 38(3): 387-399.
Battese, G. E., & Coelli, T. J. (1992). Frontier production
functions, technical efficiency and panel data: with application to paddy farmers
in India. Journal of Productivity Analysis: 3(1-2): 153-169.
Battese, G. E., & Coelli, T. J. (1995). A model for technical
inefficiency effects in a stochastic frontier
production function for panel data.
Empirical Economics, 20(2): 325-332.
Bauer, P. W., Berger, A. N., Ferrier, G. D., & Humphrey, D. B.
(1998). Consistency conditions
for regulatory analysis of financial institutions: a comparison of frontier efficiency methods. Journal of
Economics and Business, 50(2): 85- 114.
Belotti, F., Daidone, S., Ilardi, G., & Atella, V. (2013). Stochastic
frontier analysis using Stata. The Stata Journal, 13(4): 719-758.
Bengston, G. (1965). Branch Banking and Economies of Scale. Journal of
Finance, 20(2), 312-331.
Berger, A. & Humphrey, D. (1991).
The dominance of inefficiencies over scale
and product mix economies in
banking. Journal of Monetary Economics,
28(1):117–148.
Berger, A. N., & Humphrey, D. B. (1997). Efficiency of financial
institutions: International survey and directions for future research. European
Journal of Operational Research, 98(2): 175-212.
Bogetoft, P. & Otto, L. (2010). Benchmarking with DEA, SFA, and R. Springer.
Bonin, J. P., Hasan, I., & Wachtel, P. (2005). Privatization matters: Bank efficiency in transition countries. Journal of Banking
& Finance, 29(8-9), 2155-2178.
Coelli, T., Prasada Rao, D. S., O’Donnell, C. Battese, G. (2005). An introduction
to efficiency and productivity analysis. Springer.
Coelli, T. &
Henningsen, A. (2017). Frontier:
Stochastic Frontier Analysis. R package version 1.1-2.
https://CRAN.R-Project.org/package=frontier.
Cornwell, C., Schmidt,
P., & Sickles,
R. C. (1990). Production frontiers
with cross-sectional and time-series variation
in efficiency levels.
Journal of Eco nometrics,
46(1-2): 185-200.
Ferrara, G. & Vidoli, F. (2017). Semiparametric stochastic frontier models:
A generalized additive model
approach. European Journal of Operational Research, 258(2): 761-777.
Ferro, G., León, S., Romero, C., & Wilson, D. (2013). Eficiencia del
sistema banca- rio argentino
(2005–2011), Anales XLVIII Reunión Anual de la Asociación Argentina de
Economía Política. Rosario, Argentina: Universidad Nacional de Rosario.
Greene, W. (2005a). Reconsidering heterogeneity in panel data estimators
of the stochastic frontier model.
Journal of Econometrics, 126(2):
269-303.
Greene, W. (2005b). Fixed and random effects in stochastic frontier
models. Journal of Productivity Analysis, 23(1): 7-32.
Han, C., Orea, L., & Schmidt, P. (2005). Estimation of a panel data
model with parametric temporal variation in individual effects. Journal of
Econometrics, 126(2): 241-267.
Henningsen, A. & Kumbhakar, S. (2009). Semiparametric stochastic
frontier analysis: An application to Polish farms during transition. In
European Workshop on Efficiency and Productivity Analysis
(EWEPA) in Pisa, Italy, June (Vol. 24).
Henningsen, A. (2018). Introduction to Econometric Production Analysis
with R (second edition). Collection
of Lecture Notes. Department of Food and Resource Economics, University of Copenhagen.
Isik, I., & Hassan, M. K. (2002).
Cost and profit
efficiency of the Turkish banking
in dustry: An empirical
investigation. Financial Review,
37(2), 257-279.
Jondrow, J., Lovell,
C. K., Materov, I. S., & Schmidt,
P. (1982). On the estimation of technical
inefficiency in the stochastic frontier production function model. Journal of Econometrics, 19(2-3):
233-238.
Kumbhakar, S. C.
(1990). Production frontiers, panel data, and time-varying technical inefficiency. Journal of Econometrics, 46(1-2): 201-211.
Kumbhakar, S. C., Park, B. U., Simar, L., & Tsionas, E. G. (2007).
Nonparametric stochastic frontiers: a
local maximum likelihood approach. Journal of Econometrics, 137(1):
1-27.
Kumbhakar, S. C., Lien, G., & Hardaker, J. B. (2014). Technical
efficiency in competing panel data models: a study of Norwegian grain farming. Journal
of Productivity Analysis, 41(2): 321-337.
Lee, Y. H.,
& Schmidt, P. (1993). A production
frontier model with flexible temporal variation in technical efficiency.
En The Measurement of Productive Efficiency: Techniques and Applications. H.
O. Fried, C. A. Knox Lovell, and S. S. Schmidt (eds.),
237–255. New York:
Oxford University Press.
Lovell, C. A. K. (2003).
The decomposition of Malmquist productivity indexes. Journal of Productivity Analysis, 20(3): 437-458.
Meeusen, W. & van den Broeck, J. (1977). Efficiency
estimation from Cobb-Douglas production function with composed error. International
Economic Review, 18: 435-444.
Pitt, M. M., & Lee, L. F. (1981). The measurement and sources of
technical inefficiency in the Indonesian weaving industry. Journal of
Development Economics, 9(1): 43-64.
Schmidt, P. & Lovell, C. A. K. (1979). Estimating technical and allocative inefficiency relative to stochastic
production and cost functions, Journal of Econometrics, 9(3): 343-366.
Schmidt, P., & Sickles, R. C. (1984). Production frontiers and panel
data. Journal of Business &
Economic Statistics, 2(4):
367-374.
Sealey, C. & Lindley, J. T. (1977). Inputs, Outputs and a Theory of
Production and Cost at Depositary
Financial Institutions. Journal of Finance, 32(4), 1251- 1266.
Surroca, J., Prior, D. & Tribo Gine, J. A. (2016). Using panel data
DEA to measure CEOs' focus of
attention: An application to the study of cognitive group membership and performance. Strategic
Management Journal, 37(2): 370- 388.
Vidoli, F. & Ferrara,
G. (2015). Analyzing
Italian citrus sector by semi-nonparame tric frontier efficiency
models. Empirical Economics, 49(2):
641-658.
Weill, L. (2004). Measuring
cost efficiency in European banking: A comparison of frontier techniques. Journal of Productivity Analysis, 21(2), 133-152.
Williams, J. (2012). Efficiency
and market power in Latin American banking.
Jour- nal of Financial Stability, 8(4),
263-276.
[1] Por
ejemplo, Bauer, et al. (1998) incluye 683 bancos estadounidenses; Weill (2004)
trabaja con 688 bancos europeos; Bonin, et al., (2005) considera 225 bancos de
11 países de Europa del Este; Isik & Hasan (2002) toman 139 bancos
comerciales de Turquía y Williams (2012) tiene en cuenta 419 bancos comerciales
de 4 países latinoamericanos.
[2] Este
aspecto resulta fundamental en un análisis de eficiencia técnica orientada a
costos debido a la naturaleza misma del enfoque SFA. Si la descomposición del
término de error se basa, por un lado, en el error aleatorio tradicional cuya
distribución es normal y, por otra parte, en el término de ineficiencia el cual
tiene una distribución asimétrica, entonces es de esperarse que la distribución
de los residuos de la estimación de la frontera tenga un sesgo a derecha en
caso de presencia significativa de ineficiencias en costos.
[3] La
decisión sobre qué variables utilizar está respaldada fundamentalmente por la
literatura empírica. La definición de los costos, outputs y precio de inputs son
las mismas que los estudios de SFA orientado a costos citados en este trabajo
(véase sección de revisión de la literatura empírica). En tales trabajos
citados, este criterio para definir los inputs y outputs surgieron de una
modificación del enfoque de intermediación originalmente propuesto por Sealey
& Lindley (1977). Este enfoque, junto con el enfoque de producción
(Benston, 1965), son los más utilizados en la literatura sobre la industria
bancaria para describir el proceso productivo de los bancos y se diferencian
principalmente en la manera en que tratan los depósitos. El primero mira a los
depósitos como un input mientras que el segundo como un output.
 Revista de Economía y Estadística | Vol. LIX | N° 1 | 2021 | pp. 37-60 | ISSN 0034-8066 | e-ISSN 2451-7321|
Revista de Economía y Estadística | Vol. LIX | N° 1 | 2021 | pp. 37-60 | ISSN 0034-8066 | e-ISSN 2451-7321| ![]() Esta obra está bajo una Licencia Creative Commons
Atribución-No Comercial-Sin Derivar 4.0 Internacional
Esta obra está bajo una Licencia Creative Commons
Atribución-No Comercial-Sin Derivar 4.0 Internacional