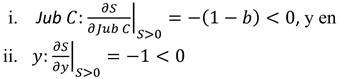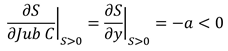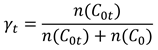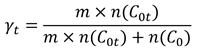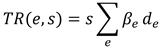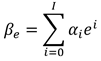Revista de Economía
y Estadística | Vol.LXI | N°1 | 2023 | pp. 11-42 | ISSN 0034-8066 | e-ISSN
2451-7321
Revista de Economía
y Estadística | Vol.LXI | N°1 | 2023 | pp. 11-42 | ISSN 0034-8066 | e-ISSN
2451-7321
Instituto de Economía y Finanzas | Facultad de Ciencias Económicas |
Universidad Nacional de Córdoba
http://www.revistas.unc.edu.ar/index.php/REyE
 Esta
obra está bajo una Licencia Creative Commons
Atribución-No Comercial-Sin Derivar 4.0 Internacional
Esta
obra está bajo una Licencia Creative Commons
Atribución-No Comercial-Sin Derivar 4.0 Internacional
Un pilar 0 para la seguridad social
uruguaya*,**
A pillar 0 for Uruguay's
social security system
Álvaro Forteza
Departamento de Economía, FCS-UDELAR (Montevideo, Uruguay)
alvaro.forteza@cienciassociales.edu.uy
Resumen
En mayo de
2023, el gobierno uruguayo promulgó la ley 20.130 que reforma el sistema
previsional uruguayo. El título VII, relativo a “los niveles mínimos de
protección”, dispone cambios significativos en lo que usualmente, en la jerga
especializada, se denomina “pilar 0” de protección social. En el presente
documento, comparto algunas ideas sobre el pilar 0 que presenté en la comisión de expertos en seguridad
social (CESS) creada en la ley 19.889 de 2020. Propongo la creación de un
ingreso universal para adultos mayores residentes en el país, inspirado en programas similares
existentes en otros países, como son el “complemento al ingreso
garantizado” (guaranteed income supplement, GIS) de Canadá, la pensión
garantizada (pension guarantee) de Suecia y la pensión solidaria de Chile.
Estas ideas fueron un insumo, entre muchos otros, para la elaboración de las
propuestas de la CESS y posteriormente de la ley de reforma.
Palabras Clave: Seguridad social, Sistema previsional,
Pensiones, Pilar 0. Código JEL: D31, H55, I38.
Abstract
In May
2023, the Uruguayan government enacted Law 20.130 reforming the Uruguayan
pension system. Title VII, on "Minimum levels of protection",
provides for significant changes
in what is usually
referred to as "pillar 0" of social protection. In this paper, I
share some ideas about pillar 0 that I presented to the Commission of Experts
on Social Security (CESS), created by
Law 19.889 of 2020. I propose the creation of a universal income for older adults residing in the country,
inspired by similar programs in other countries, such as Canada's Guaranteed
Income Supplement (GIS), Sweden's Pension Guarantee and Chile's Solidarity
Pension. These ideas were one input, among many others, into the drafting of
the CESS proposals and later the reform law.
Keywords: Social security, Pension system, Pensions,
Pillar 0. JEL Codes: D31, H55, I38.
I.
Introducción
Este documento contiene una propuesta de una prestación
previsional no contributiva que presenté en 2021 en el marco de los trabajos
preparativos para la reforma previsional de Uruguay. Esta propuesta sirvió de insumo para la reforma aprobada en
2023, pero difiere en varios aspectos del régimen finalmente aprobado.
Esta propuesta apunta
a fortalecer la protección social
de los adultos mayores en un contexto
de crecientes desafíos para la cobertura de los programas contributivos ante
los cambios que se están produciendo en el mundo del trabajo y en la
demografía.
La propuesta que presento en este documento no es original.
Es una variante de lo que en la literatura se conoce como un pilar 0 (Holzmann
y Hinz, 2005; Holzmann et al, 2000). Tiene relación con las propuestas de renta básica universal (Van Parijs, 1995)
e impuesto negativo a la renta (Friedman, 1962) pero a diferencia de éstas, el
pilar 0 se orienta casi exclusivamente a la protección de los adultos mayores y
se articula con los sistemas de jubilaciones y pensiones. Viñales (2021) propone
una renta universal en la vejez para
Uruguay que guarda relación con la que presento en este documento, pero que
difiere en algunos aspectos importantes.
El objetivo central del pilar 0 es el fortalecimiento de la
red de protección social. Es un componente central en el objetivo de alivio de
la pobreza en la tercera edad, que es usualmente considerado uno de los
objetivos centrales de los programas previsionales. El interés en este
instrumento ha crecido a raíz de las limitaciones que muestran los programas
exclusiva- mente contributivos para lograr adecuadas coberturas en la vejez
(Forteza et al 2009; Gill et al 2005; Holzmann et al, 2009; Packard et al,
2003; Rofman y Oliveri, 2011).
La propuesta intenta articular mejor los componentes no
contributivos que ya existen hoy en la seguridad social uruguaya con los componentes
contributivos del sistema. Un problema fundamental del actual diseño de los
programas contributivos es que tratan mal a personas con historias de
contribución incompletas, típicamente personas de escasos recursos (Bucheli et
al 2010, Forteza et al
2011). Hasta la flexibilización aprobada en 2008, una persona que hubiera contribuido, por ejemplo, 34 años
al Banco de Previsión Social (BPS)
sólo habría accedido a una jubilación contributiva a los 70 años,
a través del programa llamado jubilación por edad avanzada. La reforma de 2008
redujo la brecha, al reducir de 35 a 30 los años requeridos para acceder a la jubilación común a los 60 años de
edad y al reducir la edad de jubilación por edad avanzada a los 65 años. Pero
la brecha sigue existiendo. Personas con historias de contribución fragmentadas
reciben un tratamiento desventajoso de los programas previsionales
contributivos (Forteza y Rossi 2013). La articulación del pilar 0 con pilares
contributivos con mayor equidad actuarial que la actual permitiría dar un mejor
tratamiento a estas personas.
Esta propuesta también
aspira a lograr una mayor integración de los programas previsionales del país y lograr una mayor equidad.
El pilar 0 tiene vocación de
universalidad. Puede articularse con el programa del BPS-AFAPs, pero también con los restantes programas que existen
en el país. Existiendo el piso de
protección social que supone este pilar, no habría razones para mantener otros subsidios que actualmente benefician en forma desigual a
distintos programas. Varios países tienen un componente de este tipo en su
sistema previsional, incluyendo el “complemento al ingreso garantizado” (guaranteed income supplement, GIS)
de Canada, la pensión garantizada (pension guarantee)
de Suecia y la pensión solidaria de Chile. La
propuesta que se presenta en este documento toma varios elementos de estos
programas.
II. Presentación informal del pilar 0
En esta sección
presento informalmente la propuesta.
A los efectos de facilitar la
comprensión, supongo algunos valores de los parámetros del sistema. Claramente,
la propuesta consiste en un diseño y no en los valores de los parámetros elegidos con fines exclusivamente expositivos.
En la siguiente sección presento el
diseño en un formato general.
Los principios fundamentales son los siguientes:
1. Todos los individuos tienen acceso a
un ingreso mínimo garantizado (IMIN) a los 65 años de edad. Es decir que una
persona sin aportes recibe IMIN a los 65. En las simulaciones presentadas
supuse que IMIN es igual a la pensión vejez vigente en agosto de 2021, es decir
$13.035.
2. Se
reconoce el esfuerzo
contributivo: personas con contribuciones a la seguridad social reciben jubilaciones
mayores a IMIN. Las jubilaciones con subsidio son iguales a IMIN más dos
tercios de la jubilación contributiva que corresponde de acuerdo a las
contribuciones realizadas.
3. Las jubilaciones con subsidio están
topeadas por el ingreso máximo con aporte solidario (IMAS). Quienes tengan
derecho a jubilaciones contributivas financiadas exclusivamente con los aportes
personales y patronales
mayores a IMAS reciben su jubilación contributiva.
4. Si la persona tiene otros ingresos,
se deducen del subsidio. De este modo, el programa garantiza que todos los
beneficiarios tienen un ingreso igual o mayor a IMIN, pero nadie que tenga
ingresos no previsionales mayores recibirá subsidio.
5.
Los supuestos anteriores implican
que:
o IMAS es igual a tres veces IMIN, es decir $39.105, y
o la jubilación a recibir nunca será
inferior a la jubilación que puede financiarse con los aportes personales y
patronales realizados.
A modo de ejemplo, supongamos que, a valores de 2021, las
contribuciones realizadas por una persona sólo permiten financiar una
jubilación contributiva de $1.000.
La jubilación con subsidio que recibirá es
13.035 + 1.000 × 2/3 = 13.702
Lo mismo puede calcularse como:
1.000 + 13.035 × [(39.105 - 1.000)/39.105] = 13.702
El segundo sumando en esta última expresión es el monto del
subsidio, igual en este ejemplo a $12.702.
Otra persona contribuyó más y adquiere derechos a una
jubilación contributiva de $20.000. Si bien esta jubilación supera al ingreso
mínimo garantizado ($13.035), no alcanza al ingreso máximo con subsidio
($39.105). Por lo tanto, tiene derecho a un complemento a su jubilación. La
jubilación con complemento de esta persona será:
20.000 + 13.035 × [(39.105 - 20.000)/39.105] = 26.368
Considero ahora un caso de una persona que tiene derecho a
una jubilación contributiva igual a $39.104, es decir un peso menos que IMAS.
Tiene derecho a un complemento muy pequeño:
39.104 + 13.035 × [(39.105 - 39.104)/39.105] = 39.104,3
Es decir que esta persona no obtiene casi subsidio.
Finalmente, por diseño del pilar 0, una persona que tiene derecho a una jubilación contributiva
igual o mayor a IMAS ($39.105), obtiene su jubilación contributiva y no recibe
subsidio.
III. Una presentación formal general y algunas variantes
Son beneficiarios del programa todos los residentes con una
edad mínima (em) y condición de residencia a determinar.
Defino primero la jubilación financiada con los aportes,
lo que en esta nota llamaré Jub C, por
jubilación contributiva. El pilar 0 puede articularse con pilares contributivos
de reparto, ahorro individual, ahorro colectivo y mixtos. Sólo excepcionalmente
se suma a prestaciones con algún componente no contributivo, ya que uno de los
objetivos fundamentales del programa es transparentar los subsidios y
direccionarlos de acuerdo a fines bien definidos. Entonces, más allá de que el régimen
financiero de los pilares
contributivos sea reparto, capitalización o mixto, las Jub C que
considero aquí son financiadas con contribuciones especiales de seguridad social.
Defino luego un ingreso mínimo en la vejez, IMIN, que es el
ingreso mínimo por todo concepto que una persona
de e o más años de edad va
a percibir en el país, y un IMAS, que es el ingreso máximo subsidiado. La
jubilación a pagar entonces resulta ser la siguiente:
o más años de edad va
a percibir en el país, y un IMAS, que es el ingreso máximo subsidiado. La
jubilación a pagar entonces resulta ser la siguiente:
Jub = Max {Jub C;
IMIN +
b×Jub C ̵ y} (1)
Donde:
y
= otros ingresos
en la vejez (ingresos del trabajo después
de jubilado, rentas, etc.).
Lo mismo puede escribirse de la siguiente
manera:
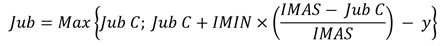 (2)
(2)
Este diseño implica varias cosas:
a)
Nadie cobra menos que su Jub C: Jub ≥ Jub C.
b)
Nadie tiene un ingreso
en la vejez inferior a IMIN: Jub + y ≥ IMIN.
c)
La jubilación es cero si: (i) Jub C=0 y, además, (ii) y ≥ IMIN.

d)
El subsidio a pagar desde rentas generales es:
Y, por lo tanto:
1)
S ≥ 0
2)
S ≤ IMIN.
3)
Es decreciente (linealmente) en:
El diseño implica
por lo tanto un impuesto
implícito con tasa igual
a (1-b) sobre las contribuciones y a 1 sobre los ingresos no previsionales en la vejez.
En la figura 1 represento este pilar 0.
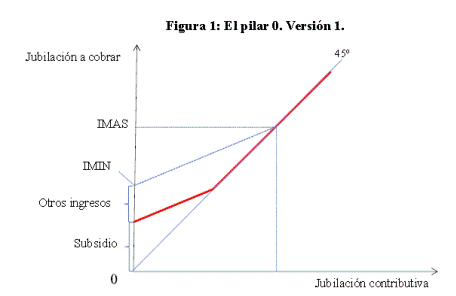
Nota: La figura
representa la jubilación a cobrar para distintos valores de la jubilación
contibutiva financiada exclusivamente con los aportes personales y patronales y con un nivel fijo de otros
ingresos. Cambios en la jubilación contributiva implican desplazamientos sobre
la curva y cambios de los otros
ingresos implican desplazamientos de la curva.
III.a Un pilar no
contributivo siguiendo el esquema
canadiense de la GIS
Canada tiene dos componentes en su programa no contributivo,
la OAS y la GIS. La OAS (old age security) son 600 dólares que se pagan a todos
los residentes. A esto se agrega la GIS o guaranteed income
supplement. El ingreso garantizado es aproximadamente 960 dólares (lo calculo
como 18.744/12 - 600, donde 18.744 es el ingreso al que el suplemento se hace
cero). La suma de estos dos componentes implica que nadie con 65 años o más
recibirá menos de 1.560 dólares.
El GIS es, como el nombre lo indica, un suplemento para llegar a un ingreso meta o garantizado. El
suplemento se reduce si la persona tiene otros ingresos, pero esa reducción no
es uno a uno. Por cada peso adicional de
ingreso, el suplemento se reduce entre 0,25 y 0,50, dependiendo de la franja de
ingresos. A continuación presento una versión del pilar 0 inspirada en ese
esquema.
Jub0 = Max { 0; IMIN - a ×(Jub C + y)
}
Donde: 0 ≤ a ≤ 1 e y representa otros
ingresos que la persona pueda tener cuando está jubilado[1]
La jubilación total es la suma de la jubilación
del pilar 0 y la jubilación contributiva:
Jub = Jub0 + Jub C
Y, por lo tanto:
Jub = Max { Jub C; IMIN +(1 - a) × (Jub C - ay) }
Y, finalmente, el ingreso en la vejez es:
Jub + y = Max { Jub C + y; IMIN + (1 - a) × (Jub C + y)
}
Algunas propiedades:
a)
Nadie cobra una jubilación
menor a su Jub C: Jub ≥ Jub C
b)
Nadie tiene un ingreso en la vejez inferior
a IMIN:
Jub + y ≥ IMIN +(1- a) × (Jub C + y) ≥IMIN.
c)
La jubilación es cero si: (i) Jub C = 0 y, además, (ii) y ≥ IMIN/a.
d)
El subsidio a pagar desde rentas generales es S = Jub0.
Y, por lo tanto:
1.
S ≥ 0
2.
S ≤ IMIN
3.
S = 0, si (Jub C + y) ≥ IMIN/a
= IMAS[2]
4. Es decreciente (linealmente) en Jub C y en y:
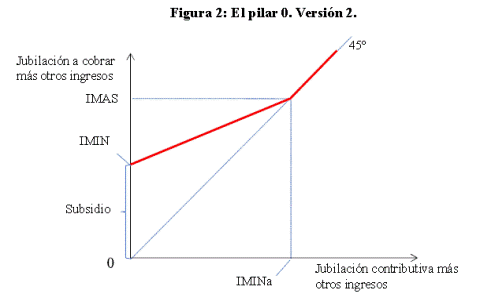
A diferencia de
la versión anterior del pilar 0, en esta versión la tasa del impuesto implícito
es la misma para los ingresos previsonales y no previsionales. Además la tasa del impuesto para los
ingresos no previsionales es menor en esta versión, por lo que desincentiva
menos los ingresos después del retiro
que la versión anterior.
IV. Simulaciones
En esta sección presento algunas simulaciones del programa
realizadas con los parámetros usados en la sección 2. En la subsección IV.1,
simulo historias individuales de contribución y analizo cómo opera el programa
en esos casos individuales. Las historias de contribución son solamente
ilustrativas y no pretenden ser representativas de la población
del país o de la población amparada por algún
programa previsional particular. En la subsección IV.2 presento simulaciones
realizadas a partir de microdatos del BPS.
IV.1.
Simulación con historias
escogidas de contribución
En los escenarios A a F, el trabajador gana el salario
mínimo a los 20 años, si trabaja a esa edad, y gana
el mínimo multiplicado por los coeficientes de movilidad salarial estimados por
el BPS, si trabaja a otras edades. En algunos de estos escenarios empieza a
contribuir a los 20 y en otros empieza más tarde. En los escenarios G y H gana 2
y 4 veces el mínimo
a los 20 años.
Los escenarios A a F difieren en las carreras de
contribución. En A y B, el trabajador tiene una densidad de
cotización casi 0, ya que aporta exclusivamente a los 20 y a los 64 años,
respectivamente. En C tiene una densidad del 100% entre los 20 y los 64 años de
edad, cuando decide retirarse. En los escenarios D, E y F tiene una densidad de
60% - lo que implica que contribuye 27 años-,
pero con historias
de interrupción variadas:
en D empieza a aportar a los 38, en E aporta entre los 20 y los 46 y
en F aporta en varios períodos sucedidos de varias interrupciones (detalles en nota F del cuadro).
Los escenarios G y H tienen la misma densidad y perfil de
interrupciones que el escenario F.
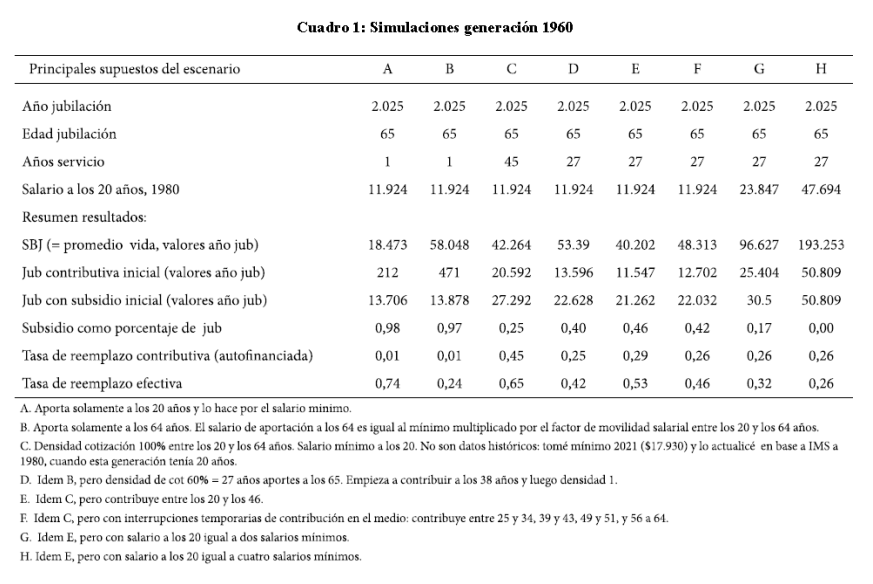
El Cuadro 1 resume los principales resultados. Los escenarios A, B y H representan casos extremos casi sin contribuciones (escenarios A y B) y con contribuciones suficientes para
financiar una jubilación igual o mayor a
IMAS (escenario H). En el primer caso, escenarios A y B, el subsidio representa
entre el 98 y el 97% de su jubilación final y en el último es cero (ver la fila
“Subsidio como porcentaje de Jub” en el cuadro 1). Los restantes escenarios son
casos intermedios en este aspecto.
El individuo del escenario C tiene una historia laboral muy
completa, con 100% de densidad de cotización y 45 años de aportes al momento de
jubilarse. Sin embargo, su jubilación contributiva autofinanciada ($20.592) es inferior al ingreso máximo con subsidio
y, por lo tanto, tiene derecho a un subsidio
que, en este caso, representa 25% de la jubilación final.
Los individuos de los escenarios D a H tienen densidad de
cotización 60% o, lo que es lo mismo,
contribuyen 27 de los 45 años potenciales (de 20 a 64). Consecuentemente, las tasas de reemplazo son
menores a las del escenario con densidad 100%.
Los escenarios D a F tienen igual ingreso y densidad de
cotización, pero con distintas historias de contribución. El subsidio representa entre 40 y 46% de la jubilación con que recibirán
estos individuos.
Los individuos del escenario G reciben menor subsidio
debido a que sus jubilaciones contributivas son mayores, como consecuencia de
que sus salarios duplican a los de los escenarios anteriores. Finalmente, en el
escenario H no hay subsidio y la persona
se jubila con su jubilación
contributiva.
La tasa de reemplazo contributiva varía desde casi cero
(1%) en los escenarios A y B hasta 45% en el escenario C. Pero la tasa de
reemplazo efectiva -el cociente entre la jubilación efectivamente cobrada y el
salario básico jubilatorio- difiere
marcadamente de la contributiva. El escenario A es el
que presenta mayor tasa efectiva (74%) a pesar de ser uno de los dos con menor tasa contributiva (1%).
Estas simulaciones no permiten decir qué cantidad de
personas se beneficiarían de un pilar 0 como el descrito. Para responder a esa
pregunta hay que trabajar
con los microdatos del BPS y/o de la DGI (y eventualmente de otras cajas). De todos
modos, es bastante inmediato ver que el programa beneficiaría a un elevado
porcentaje de la población. De hecho, con
los números considerados en este ejercicio, probablemente el programa sea
prácticamente universal.
Siguen algunos cálculos muy preliminares para dar una idea de los
órdenes de magnitud involucrados.
·
Con tasas
de reemplazo (contributivas) del orden del 25%, más del ochenta por ciento de
la población de entre 20 y 64 años (1.666.836 personas) no llegaría a pagar
contribuciones suficientes para financiar una pensión vejez a los 65 años
(calculado a partir de ECH 2019)[3]
Son las personas con ingresos
inferiores a 4×13.035=52.140.
·
Quedarían
cubiertos por el pilar 0 todas las personas que tuvieran un salario promedio a
lo largo de su vida inferior a 4×39.105=156.420. Según la encuesta continua de
hogares 2019, casi toda la población tiene ingresos inferiores a ese umbral y,
por lo tanto, estarían en principio en condiciones de acceder a un beneficio
por este pilar.
IV.2 Simulaciones en base a microdatos
del BPS
En esta subsección, presento algunos resultados de
simulaciones de una generación de afiliados al BPS. Considero las prestaciones
que habría recibido la generación que cumple 65 años de edad en 2021 (nacida en 1956) si hubiera estado cubierta por el
pilar 0 y por un programa contributivo mixto actuarialmente justo durante toda
su vida laboral.
Supuse que los aportes personales y patronales son 22,5%,
de los cuales 7,5% se depositan en las cuentas de ahorro individual. La base
grabada son los salarios asegurados, es decir salarios
por debajo de $202.693 (ley 16.713,
a valores de mediados de 2021). En esta simulación, los fondos de ahorro
previsional rinden 3% anual y los aportes en el pilar de reparto rinden 0%
anual, ambos en términos de salarios (en otros términos, crecen 3 y 0 por
ciento más que el índice medio de salarios).
Las historias laborales se simularon usando la metodología
descrita en Bucheli et al (2010) y
Forteza et al (2011 y 2013). Todos los valores monetarios están expresados en valores
de 2021.
Por carecer de información y/o capacidad de procesamiento,
no desconté otros ingresos en el pilar 0. En otras palabras, en términos de la
ecuación ( 1), las simulaciones que siguen suponen y =0.
En el Cuadro 2 presento el ingreso promedio de contribución
de la vida (actualizado por IMS) por quintiles de ingreso en la base simulada. Estos datos solo interesan a los efectos
de dar una referencia del tipo de historias
laborales sobre las que se aplicó el sistema previsional propuesto.

En el Cuadro 3 presento la estimación de los años de aportes acumulados
a los 65 años de edad por quintiles de ingreso. Los años de aportes varían mucho
incluso al interior
de los quintiles de ingreso,
pero la media y
la mediana muestran
claramente que un porcentaje muy significativo de la población no alcanza la cantidad de años requeridos para acceder a la jubilación común (30 años).
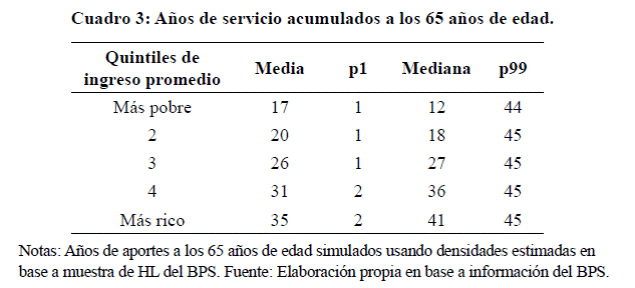
La media y la mediana de años de servicio acumulados
aumenta sensiblemente con el nivel de ingreso. Por lo tanto, los trabajadores
de menores ingresos, no sólo tienen una base contributiva más pequeña (Cuadro
2) sino que también contribuyen por menos años (Cuadro 3). Si bien estos
resultados deben tomarse
con cautela por ser el producto
de simulaciones para completar historias observadas solo parcialmente, los
resultados están básicamente en línea con lo que se ha reportado en la
literatura (ver, entre otros, Bucheli
et al 2010; Lavalleja et al 2018 y Zunino
et al 2020).[4]
En el Cuadro 4 presento un resumen de jubilaciones a cobrar, incluyendo
los pilares 0, 1 y 2. Como cabía esperar, las jubilaciones son crecientes con
el nivel de ingreso de contribución.
Cuadro 4:
Jubilaciones iniciales por nivel de ingreso
|
Quintiles de ingreso promedio
|
Media
|
p1
|
Mediana
|
p99
|
|
Más pobre
|
14.460
|
13.326
|
13.876
|
15.276
|
|
2
|
16.828
|
14.667
|
16.480
|
18.708
|
|
3
|
20.790
|
17.090
|
21.001
|
24.139
|
|
4
|
27.227
|
22.752
|
28.337
|
31.724
|
|
Más rico
|
54.004
|
40.290
|
52.447
|
66.291
|
Notas: Jubilación total promedio (BPS+AFAP) por tramos de ingreso.
El Cuadro 5 presenta una estimación de las tasas de
reemplazo resultantes. Corresponde hacer dos advertencias metodológicas
importantes para interpretar estas cifras. La primera es que la tasa de
reemplazo está definida aquí como la relación entre la jubilación inicial por
todo concepto y el salario promedio (actualizado por IMS) de contribución a lo
largo de toda la vida. Es usual que se presenten tasas de reemplazo con otras
definiciones que, si bien son tan válidas como la elegida aquí, no resultan
comparables con estas. Segundo, dado
que el pilar 0 paga una prestación aún a personas que no han realizado
contribuciones, la tasa de reemplazo no
está definida en esos casos. Por lo tanto, los valores que figuran en el Cuadro
5 refieren exclusivamente a la población que realizó contribuciones de
seguridad social.
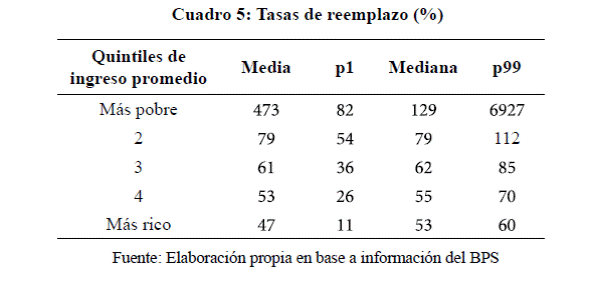
Las tasas de reemplazo son claramente decrecientes con el
nivel de ingreso, reflejando el carácter fuertemente distributivo del pilar 0
(recordar que los pilares 1 y 2 en estas simulaciones son actuarialmente
justos). El quintil de menores
ingresos obtendría, según estas simulaciones una tasa de reemplazo
mediana de casi 130%. El quintil de mayores ingresos tendría una tasa mediana
de 53%. No puede descartarse que algunos individuos obtengan tasas de reemplazo
muy pequeñas, como es el caso del percentil 1 en el nivel de ingresos más alto,
pero este resultado corresponde al caso de una persona que contribuyó muy poco
tiempo en base a ingresos elevados. Queda en el quintil de mayor ingreso
promedio, pero tiene muy escasas contribuciones y por lo tanto recibe poco más
que IMIN. Dividido por el ingreso promedio de contribución se obtiene una tasa de reemplazo muy baja.
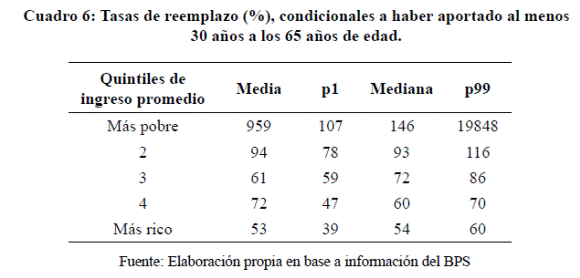
En el Cuadro 6
presento tasas de reemplazo condicionales a que las personas hayan contribuido 30 años o más a los 65. Como puede verse, las
tasas de reemplazo de quienes han
contribuido al menos 30 años no bajan de poco
menos de 40%, aún en sectores de muy
altos ingresos.
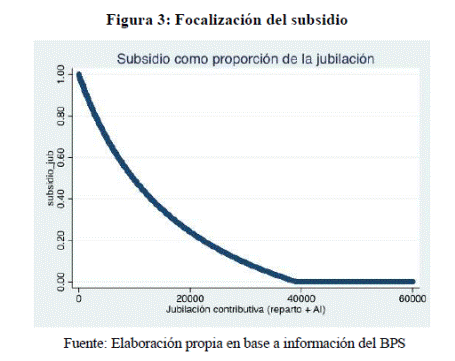
La focalización de los subsidios que ofrece este diseño
puede verse en la Figura 3. Personas
sin jubilación contributiva reciben un subsidio que equivale al 100 por ciento
de su jubilación. En este caso, la prestación es totalmente asistencial. Personas
que tienen una jubilación contributiva mayor o igual a IMAS no reciben subsidio.
V. La transición
Considero una fórmula de transición inspirada en los
convenios de seguridad social que buscan acumular derechos jubilatorios en
distintos países. Para acumular derechos se consideran las contribuciones
realizadas en todas las jurisdicciones (totalización) y se calculan
los beneficios y el costo según el
tiempo trabajado en cada jurisdicción (prorrata tempore). Apli- cado a la
transición, podemos pensar en el régimen viejo y el nuevo como dos programas aplicables en dos
jurisdicciones. La persona que contribuye antes y después de la reforma
es tratada como un trabajador migrante.
El beneficio en transición se calcula como un promedio de
los derechos adquiridos en ambos regímenes, contando la totalidad de los
aportes realizados en ambos, ponderado por el tiempo (alternativamente los
aportes realizados) en cada régimen. Si, por ejemplo, una persona contribuye 20 años en cada régimen, totalizando 40 años
de aportes, se calculan dos jubilaciones: (i) la generada con las reglas viejas
y (ii) la generada con las reglas nuevas. Ambos cálculos se realizan
con la totalidad de los aportes, los que
se hicieron bajo las viejas y las nuevas reglas. Luego se calcula un promedio
entre ambas jubilaciones, con una ponderación
de 50% en este caso ya que
la persona trabajó mitad de tiempo bajo las viejas y mitad bajo las nuevas reglas.
Algunas virtudes de este mecanismo:
•
transición gradual
y sin grandes discontinuidades;
•
reconocimiento pleno de los derechos generados.
Algunos defectos:
•
transición muy larga;
• el programa viejo podría
dejar sin beneficios a personas que no cumplen
con las condiciones de acceso, aún con
la totalización.
Acortando la transición. La transición puede
abreviarse modificando los ponderadores para promediar prestaciones. Para eso, hay que aumentar la ponderación del régimen nuevo
en la fórmula del beneficio durante la transición.
Una forma de hacerlo es la siguiente. Los años aportados en el régimen nuevo se
multiplican por m ≥ 1. El ponderador de las prestaciones bajo el nuevo régimen se calcula como los años
aumentados bajo este régimen dividido la suma de los años efectivos bajo el
viejo y los años aumentados bajo el nuevo. El parámetro m controla
exactamente la duración de la transición. Si se elige m = 1, se vuelve
al caso anterior, con prorrata tempore estricta. A medida que crece este parámetro, más
rápida es la transición. Si se
elige m muy grande, no hay transición, se pasa directamente al régimen nuevo.
Desprotección con el viejo programa. Supongo un caso en que una persona contribuye 8 años con el viejo
programa y 4 con el nuevo. Totaliza 12 años. Con el viejo programa no accede a
un beneficio contributivo, a pesar de
la totalización. Con el nuevo obtendría IMIN más dos tercios de la jubilación
financiada con esos 12 años de aportes. Si se promedian esas dos jubilaciones,
quedará con una prestación inferior a la del nuevo régimen, pudiendo incluso
ser inferior a IMIN.
Una posible solución es aplicar el pilar 0 desde el inicio
de la transición. Desventajas: (i) estaremos otorgando complemento (subsidio) a
algunas personas que ya están recibiendo subsidios
encubiertos en las tasas
de reemplazo del régimen viejo. (ii) Probablemente sea de alto costo por la
duplicación de los subsidios.
Otra solución es sustituir la jubilación del viejo régimen
por el máximo entre esa jubilación y la del nuevo y luego promediar el
resultado de ese máximo y la jubilación del nuevo prorrateando como se indicó
más arriba. De esta manera, se pondría en funcionamiento el pilar 0 inmediatamente
sin duplicar subsidios. Se estaría garantizando el ingreso mínimo desde el
primer día de la reforma.
Con esta fórmula podría ocurrir que alguien de altos ingresos se viera
beneficiado con las prestaciones del régimen nuevo desde el principio. Eso
ocurriría si la prestación autofinanciada superara a la jubilación del viejo
régimen. No parece probable que eso ocurra en la práctica, pero depende del
valor de los parámetros que se elijan.
Si eso preocupara, se podría limitar
el otorgamiento del máximo entre el régimen viejo y el nuevo a quienes
generaran beneficios menores o iguales a IMAS en
cualquiera de los dos.
Una ventaja de usar esta variante es que habilitaría a eliminar el
testimonio de testigos y el comunicado 42 inmediatamente.[5]
En el Anexo 1 desarrollo la transición formalmente.
VI. Discusión: algunos desafíos
El costo del programa depende, naturalmente, de los valores
que se elijan de los parámetros del pilar 0. El programa tiene tres parámetros:
el ingreso mínimo garantizado (IMIN), el ingreso máximo con subsidio (IMAS) y la edad de acceso (e ). El costo, pero
también la protección social, se reducen si se reducen el ingreso mínimo y/o
máximo o si se aumenta la edad de acceso.
). El costo, pero
también la protección social, se reducen si se reducen el ingreso mínimo y/o
máximo o si se aumenta la edad de acceso.
Estimaciones muy preliminares realizadas usando microdatos
de historia laboral del BPS indican que en 2021 el programa podría costar como
máximo 2,4 puntos porcentuales del
PBI, si se adoptaran los parámetros usados en la sección
2 de este documento (IMIN=13.035, IMAS = 39.105, e =65) [6] En su informe diagnóstico, la CESS estimó que el BPS recibe
aproximadamente 3,1 puntos porcentuales del PBI actualmente para contribuir al financiamiento de sus programas previsionales (IVS). Si a esta cifra se suman los recursos de
gravámenes destinados a los servicios de retiros policial y militar y al
financiamiento de las cajas bancaria (principalmente PCP) y profesional
(artículo 71 de la ley 17.738), se concluye que el costo del pilar 0 con esos valores de los parámetros es
muy inferior a lo que ya actualmente se está transfiriendo a los programas
previsionales que cubriría el pilar 0.
=65) [6] En su informe diagnóstico, la CESS estimó que el BPS recibe
aproximadamente 3,1 puntos porcentuales del PBI actualmente para contribuir al financiamiento de sus programas previsionales (IVS). Si a esta cifra se suman los recursos de
gravámenes destinados a los servicios de retiros policial y militar y al
financiamiento de las cajas bancaria (principalmente PCP) y profesional
(artículo 71 de la ley 17.738), se concluye que el costo del pilar 0 con esos valores de los parámetros es
muy inferior a lo que ya actualmente se está transfiriendo a los programas
previsionales que cubriría el pilar 0.
Una preocupación que ha surgido en discusiones en torno a
esta propuesta es la de los incentivos a contribuir. El temor es que el pilar 0
represente un desincentivo a contribuir a la seguridad social. Según este
razonamiento, algunas personas, sabiendo que tendrán acceso a un ingreso igual
a IMIN en la vejez, podrían dejar de contribuir. A mi entender, la preocupación es legítima, pero la amenaza
depende en última instancia de los valores de los parámetros que se
elijan. Un IMIN excesivamente elevado y a
edades demasiado tempranas podría tener el efecto temido.
Lamentablemente, no es fácil estimar
estos efectos empíricamente y tal esfuerzo trasciende
las posibilidades de este trabajo. No obstante, con parámetros en los órdenes
de magnitud de los usados en este documento
no parece probable que se produzca un fuerte desincentivo a contribuir. Uruguay
ya tiene una pensión no contributiva de $13.035 a los 70 años (pensión vejez del BPS) y otra prestación de asistencia a la vejez
del plan de Equidad-Mides con
acceso a los 65 años. El pilar 0 podría sustituir estos dos programas. No veo
razones para pensar que debería generar mayores desincentivos a contribuir que
estos programas.
Adicionalmente, los programas
supuestamente contributivos que hay en Uruguay hoy tienen un
importante componente no contributivo que generan, al menos teóricamente, mayores desincentivos a la contribución que el pilar 0 propuesto en
este documento. El caso más obvio es el de la jubilación mínima. Como es bien sabido,
una jubilación mínima implica
un impuesto del cien por ciento en el margen a las contribuciones. El pilar
0 tendría un impuesto implícito menor. Si se usaran los valores de los
parámetros considerados en este documento para construir ejemplos, el impuesto
implícito con el pilar 0 sería de 33%. Habría entonces una reducción del 67 por
ciento en la tasa del impuesto implícito a las contribuciones de la población
beneficiaria de la jubilación mínima.
Por otra parte,
el actual diseño del pilar de reparto
administrado por el BPS contiene un impuesto implícito a seguir
trabajando una vez generada la causal jubilatoria variable entre individuos
pero que alcanza una importante magnitud en muchos casos (Alvarez et al 2010).
Esto implica un castigo financiero a quien decide postergar el retiro. Si bien
no hay evidencia clara de que ese impuesto
implícito a seguir trabajando haya incidido en forma significativa en la decisión
de retiro de los uruguayos, hay evidencia de que impuestos de similar orden de
magnitud generan reducciones estadísticamente significativas en la edad de
retiro en varios países de la OECD (Gruber y Wise 2004). Estos potenciales
desincentivos pueden eliminarse mejorando la equidad actuarial del sistema, aún
en presencia de un pilar 0 importante.
Por último, no conozco evidencia clara de que el pilar 0
esté generando desincentivos a la contribución en los países que lo aplican. Dos de
los países que tienen un pilar 0 similar al considerado en este documento son Canadá y Suecia. El programa
canadiense llamado “suplemento al ingreso garantizado” (GIS) ofrece un complemento por sobre la prestación
del programa OAS (Old Age Security) para personas cuyos ingresos estén por debajo de ciertos límites. Para ser elegible,
se debe tener 65 años o más
y residir o haber residido
en Canadá al menos 10 años desde
los 18 años de edad. En el sitio web se aclara expresamente que no
tiene requisitos de años de aportes ni de no estar trabajando.[7]
En forma similar, Suecia ofrece una pensión garantizada (pension
guarantee) a personas que carecen de una jubilación contributiva o tienen
una jubilación baja, a partir
de los 65 años de edad y con
un requisito mínimo de residencia[8]
Ambos países tienen muy bajos niveles de informalidad
laboral, sensiblemente inferiores a los que tiene Uruguay y otros países que
carecen de pilares no contributivos similares a los de Canada y Suecia. Si bien
se requerirían estudios para evaluar posibles impactos de un programa de este
tipo en la informalidad, la comparación de experiencias no sugiere que estos
programas sean un obstáculo significativo a la formalización. Al menos, está claro que no la impiden.
En América Latina, Chile introdujo un pilar 0 durante el primer
gobierno de Michele Bachelet. El llamado pilar solidario “entrega
Pensiones Básicas
Solidarias (PBS) a quienes nunca cotizaron en el Sistema de Pensiones. También Aportes
Previsionales Solidarios (APS) a los trabajadores que ahorraron muy poco, con
el fin de mejorar su
pensión”[9]
. Hasta donde conozco, no hay evidencia de que el pilar solidario haya
provocado un aumento de la informalidad en Chile.
VII. Referencias bibliográficas
Alvarez, I.; da Silva, N.; Forteza, A. & Rossi, I. (2010). ¿Qué incentivos
al retiro genera la seguridad social? El caso uruguayo.
Cuadernos de Economía, 47, 217-247
Bene,
Nicolás (2021). Densidad de cotización al BPS. CESS, Nota técnica No 5.
Bucheli, M.; Forteza, A. & Rossi, I. (2010). Work history and the access to contributory
pensions. The case of Uruguay. Journal of Pension Economics and Finance, 2010,
9, 369-391
Forteza, A.; Lucchetti, L.
& Pallares-Miralles, M. (2009). Measuring the Coverage Gap, en: Holzmann, R.; Robalino, D. A. & Takayama, N. (Eds.) Closing the Coverage Gap. The Role of Social Pensions and Other
Retirement Income Transfers. The World Bank.
Forteza, A.; Apella, I.; Fajnzylber, E.; Grushka, C. O.; Rossi, I. &
Sanroman, G. (2011). Contributions to Social Security in Argentina, Chile and
Uruguay: Densities, Transitions and Duration. Económica, LVII, 127-163
Forteza, A. y Rossi, I. (2013). NDC vs NDB for Infrequent Contributors.
IN: Holzmann, R.; Palmer, E. & Robalino, D. A. (Eds.): Nonfinancial Defined Contribution Pension Schemes
in a Changing Pension World, The World Bank.
Friedman,
M. (1962). Capitalism and Freedom. The University of Chicago Press.
Gill, I.; Packard,
T. y Yermo, J. (2005). El futuro de la seguridad social en America
Latina. The
World Bank.
Gruber, J. y Wise, D. A. (Eds.)
(2004). Social
Security Programs and Retirement Around the World. Micro-Estimation. The University of Chicago Press.
Holzmann, R.; Packard, T. y Cuesta, J. (2000). Extending Coverage in Multi-Pillar Pension Systems: Constraints and
Hypotheses, Preliminary Evidence and Future Research Agenda. Social Protection
Discussion Papers and Notes 21303, The World Bank.
Holzmann, R. y Hinz, R. (2005). Old Age Income Support in the 21st Century:
an International Perspective on Pension Systems and Reform. The World Bank.
Holzmann, R.; Robalino,
D. A. y Takayama, N. (Eds.) (2009).
Closing the Coverage Gap. The Role of Social Pensions
and Other Retirement Income Transfers. The World Bank.
Lavalleja, M.; Rossi,
I. y Tenembaum, V. (2018).
La flexibilización de las condicio- nes de acceso a las jubilaciones en el Uruguay.
Serie Estudios y Perspectivas.
Oficina de la CEPAL Montevideo.
Packard, T.; Shinkai, N. y Fuentes, R. (2003). The Reach of Social Security in Latin
America and the Caribbean. The
World Bank.
Parijs, P. (1995). Real
Freedom for All: What (if anything) can justify capitalism?
Clarendon Press, Oxford.
Rofman, R. y Oliveri, M. L. (2011). La cobertura de los sistemas
previsionales en América Latina: conceptos e indicadores. The World Bank.
Viñales, G. (2021). Análisis y fundamentación
general, diseño tentativo, estimación preliminar de los costos y posibles modos
de financiamiento, de una renta universal en la vejez. Informe de consultoría
para UNFPA.
Zunino, G.; Caporale, F.; Pereira,
M. y Souto, A. (2020). Densidad de
Cotizaciones, Historias Laborales y Rendimientos Jubilatorios en el Sistema
de Seguridad Social de Uruguay. Cinve.
VIII. Anexo 1: La transición
Los beneficios a otorgar a personas que contribuyeron antes y después de la reforma se calculan como un
promedio ponderado de los beneficios a los que habrían accedido de mantenerse
el viejo régimen y los que habría ganado en el nuevo si hubiera contribuido
todo el tiempo en cada uno de los dos.
JubT = γ
= γ JubN
JubN + (1 - γ
+ (1 - γ )JubV
)JubV * (3)
* (3)
donde JubT , JubN
, JubN y JubV
y JubV * representan las jubilaciones de
transición, nueva y “vieja”, respectivamente, en t; y γ
* representan las jubilaciones de
transición, nueva y “vieja”, respectivamente, en t; y γ [0,1] es el ponderador del régimen nuevo en
[0,1] es el ponderador del régimen nuevo en
Prorata tempore estricta:
donde n(C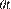 ) y n(C
) y n(C ) son los
cardinales de los conjuntos de contribuciones mayores a cero, entre la reforma
y t(C
) son los
cardinales de los conjuntos de contribuciones mayores a cero, entre la reforma
y t(C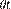 ), y antes de la reforma (C
), y antes de la reforma (C ),
respectivamente. Estas variables y, por lo tanto, la ponderación varía entre
individuos, dependiendo de la historia de contribuciones.
),
respectivamente. Estas variables y, por lo tanto, la ponderación varía entre
individuos, dependiendo de la historia de contribuciones.
Naturalmente que:
(i) n(C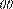 )
= 0 Þ γ
)
= 0 Þ γ = 0. Es decir que en el momento
de la reforma el ponderador es cero y por lo tanto la jubilación es la del viejo
régimen JubT
= 0. Es decir que en el momento
de la reforma el ponderador es cero y por lo tanto la jubilación es la del viejo
régimen JubT = JubV
= JubV *.
*.
(i) n(C ) = 0 Þ γ
) = 0 Þ γ = 1 Es decir que una persona que no hizo
contribuciones antes de la reforma (antes de t = 0) recibirá la
jubilación que le corresponda de acuerdo al régimen nuevo.
= 1 Es decir que una persona que no hizo
contribuciones antes de la reforma (antes de t = 0) recibirá la
jubilación que le corresponda de acuerdo al régimen nuevo.
Como puede verse, la ponderación γ es idiosincrática de cada individuo, dependiendo de la historia
de contribuciones. Sin perjuicio de ello, es
evidente que todos los integrantes de cohortes nacidas
(o que acceden a la edad mínima para trabajar) después de la reforma
tendrán γ
es idiosincrática de cada individuo, dependiendo de la historia
de contribuciones. Sin perjuicio de ello, es
evidente que todos los integrantes de cohortes nacidas
(o que acceden a la edad mínima para trabajar) después de la reforma
tendrán γ = 1. Para alivianar la notación, no estoy poniendo
ningún índice que recuerde que γ
= 1. Para alivianar la notación, no estoy poniendo
ningún índice que recuerde que γ varía
a través de individuos. Si esto generara alguna ambigüedad, se podría agregar
un subíndice para indicar el individuo i.
varía
a través de individuos. Si esto generara alguna ambigüedad, se podría agregar
un subíndice para indicar el individuo i.
Un problema de (4) es que la transición resulta muy larga. Mientras
haya personas que hayan registrado un período de contribuciones bajo las viejas reglas habrá transición. Es claro que el impacto
en el agregado de unos pocos
que queden con una pequeña proporción del régimen viejo será mínimo, pero aún
así la transición es larga. Por ejemplo, si las historias promedio de
contribución tuvieran 30 años, 15 años después de la reforma las reglas del viejo régimen tendrían
todavía aproximadamente igual peso que
las del nuevo en las nuevas jubilaciones.
Acortando la transición. Considero dos opciones:
i)
Ponderar
más las contribuciones bajo el nuevo régimen. Sustituyo la ecuación ( 4) por la
siguiente:
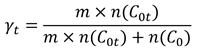 (5)
(5)
donde m
≥ 1. Bajo esta expresión la ponderación del nuevo
régimen es creciente en el
multiplicador m. Si bien esta expresión no cambia el número
de períodos en los
que hay transición, reduce el peso de
las viejas reglas en el cálculo de
todas las jubilaciones posteriores a la reforma.
ii) Ponderadores basados en una función logística.
Sustituyo la ecuación (4) por
 (6)
(6)
donde n es el parámetro que controla la duración de
la transición[11].
Cuanto menor es el parámetro
n, más corta es la
transición.[12]
El problema de la potencial desprotección con el viejo
programa puede resolverse introduciendo el pilar 0 desde el inicio, pero con
los inconvenientes que mencioné más arriba. Una fórmula que posiblemente
funcione mejor es la siguiente:
JubV * = Max { JubV
* = Max { JubV , Min{IMAS,JubN
, Min{IMAS,JubN }}
(7)
}}
(7)
donde JubV es la jubilación que se obtendría con las reglas
del viejo régimen, suponiendo que todas las contribuciones se hubieran hecho
bajo esas reglas. La ecuación (7)
determina que la jubilación del viejo régimen se sustituye por la mayor entre
la jubilación generada bajo esas reglas y las que se obtendrían con las nuevas
reglas siempre que esta última no sea mayor a IMAS. Con esto logro dos cosas:
es la jubilación que se obtendría con las reglas
del viejo régimen, suponiendo que todas las contribuciones se hubieran hecho
bajo esas reglas. La ecuación (7)
determina que la jubilación del viejo régimen se sustituye por la mayor entre
la jubilación generada bajo esas reglas y las que se obtendrían con las nuevas
reglas siempre que esta última no sea mayor a IMAS. Con esto logro dos cosas:
 Ningún beneficiario del pilar 0 puede obtener durante la transición
menos de lo que obtendría en el nuevo régimen.
Ningún beneficiario del pilar 0 puede obtener durante la transición
menos de lo que obtendría en el nuevo régimen.
 Quienes tienen derechos
generados por el viejo régimen
superiores al ingreso máximo con aporte solidario (IMAS) siguen
computando esos derechos en la fórmula de la transición.
Quienes tienen derechos
generados por el viejo régimen
superiores al ingreso máximo con aporte solidario (IMAS) siguen
computando esos derechos en la fórmula de la transición.
Lo principal de esta variante contenida en (7) es, naturalmente, el
primer punto. Supongamos un caso de una persona con bajas contribuciones
totales que no le permiten acceder a una jubilación contributiva en el viejo
régimen. Podría ser el ejemplo que puse en el cuerpo principal de este
documento: 8 años de contribución bajo las viejas reglas y 4 bajo las nuevas.
En este caso, JubV =0, pero como JubN
=0, pero como JubN > IMIN > 0, JubV
> IMIN > 0, JubV * = JubN
* = JubN . Sustituyendo en (3) obtengo que este individuo
recibiría JubT
. Sustituyendo en (3) obtengo que este individuo
recibiría JubT = JubN
= JubN aún cuando se jubilara el mismo año de la reforma. Por lo tanto,
para personas beneficiarias del complemento al ingreso
mínimo garantizado, el pilar 0 estaría operando desde el año cero de la
reforma.
aún cuando se jubilara el mismo año de la reforma. Por lo tanto,
para personas beneficiarias del complemento al ingreso
mínimo garantizado, el pilar 0 estaría operando desde el año cero de la
reforma.
De acuerdo a lo anterior, una transición con prorrata
ofrece mejor protección social si se incluye la ecuación (7), pero es
obviamente más costosa. Por lo tanto, es fundamental estimar los costos de esta
variante. Tengo la impresión que no sería demasiado caro ya que actualmente, de
una forma u otra, la población mayor de 65 está cubierta. Se trataría de
reasignar recursos.
Una ventaja de usar la variante (7) es que habilitaría a eliminar el testimonio
de testigos y el comunicado 42 inmediatamente.
Ambos mecanismos tienen por objeto garantizar el acceso a prestaciones
contributivas a gente que no lo logra
con contribuciones documentadas. El pilar
0 en
la variante de la transición
de esta ecuación produce el mismo resultado sin necesidad de acudir a testigos ni al comunicado 42. Para eso, habría que acordar que, a partir de la reforma, solo se
acepta prueba documental de contribuciones realizadas antes de 1996. Por
supuesto que puede aplicarse la fórmula (7) manteniendo testigos y 42, pero me
parece un buen momento para eliminar esas soluciones al aportar una nueva. Se ha
argumentado que ambos mecanismos se usaron para lograr acceso y no para
aumentar beneficios. Si es así, ningún usuario de testigos y 42 se perjudicaría
con la fórmula que propongo. Al contrario, obtendrían un mejor resultado. Por
otra parte, aunque no es un argumento de primer orden, al BPS le simplificaría
mucho la gestión.
IX.
Anexo 2. Estimación de las tasas de reemplazo de un sistema de reparto cuasi equilibrado actuarialmente
El pilar 0 descrito absorbe
todos los recursos
provenientes de rentas generales con destino a las
prestaciones IVS. Como contraparte, el o los pilares contributivos tienen que
financiarse exclusivamente con aportes. Lo anterior se logra naturalmente en el
pilar de ahorro individual y en el pilar de reparto si es de contribución definida
(cuentas nocionales), pero no necesariamente si es de beneficios definidos. En
este anexo presento algunas ideas para un diseño de un pilar de reparto de
beneficios definidos que, aunque se aparta de la equidad actuarial, tiene el
menor desvío posible dentro de lo que permite el diseño BD (en realidad, una
subfamilia de los BD, como explico más abajo).
Respondiendo a inquietudes surgidas en la CESS, desarrollo
el modelo con un esquema de tasas de adquisición de derechos por períodos de aportes[13]. Si los períodos fueran
años, el programa tendría una tasa diferente para cada edad de retiro. Por
ejemplo, si retirándose a los 65 años con 30
años de aportes se pudiera financiar una jubilación de 30 por ciento, la
tasa de adquisición a los 65 sería
uno por ciento por año. Retirándose a la misma edad, pero con 40 años de aporte, la tasa de reemplazo sería
40 por ciento. Si en cambio la persona se jubilara a los 66, las tasas
de reemplazo y, por lo tanto, las tasas de adquisición serían mayores.
Supongamos que a los 66 la tasa de adquisición fuera 1,01. Entonces con 30 años
de aportes se obtendría una tasa de reemplazo de 30,3.
En el programa BD el contribuyente adquiere derecho a la
jubilación al alcanzar una edad mínima y cantidad de períodos de contribución.
La jubilación inicial se calcula como un SBJ multiplicado por una tasa de
reemplazo. La tasa de reemplazo se calcula como el número de períodos de
servicio multiplicado por la tasa de adquisición y esta varía con la edad de
jubilación. Los parámetros del sistema son entonces: (i) edad mínima, (ii)
número mínimo de períodos de contribución o servicio, y (iii) tantas tasas de
adquisición como edades por encima de la mínima se definan (esto depende de la grilla
de edades, es decir si se hace anual o algo más fino o más grueso).
En lo que sigue, explico esta sugerencia de cómo
instrumentar formalmente la propuesta de cálculo de la jubilación contributiva
usando las “tasas de adquisición de derechos” (accrual rates) y
considerando algunas opciones más, aunque siempre dentro de los límites de esta
propuesta.
El programa
BD debería satisfacer
las siguientes propiedades:
• La jubilación inicial es igual a una
tasa de reemplazo por un salario básico jubilatorio.
• Se accede a la jubilación
contributiva de beneficios definidos si y sólo si (i) la edad y (ii) el número
de períodos de contribución superan ciertos mínimos.
• Para cada edad de jubilación, la tasa
de reemplazo es igual a una tasa de adquisición de derechos jubilatorios
(accrual rate) multiplicada por el
número de períodos
• La tasa de reemplazo y, por lo tanto, la tasa de adquisición de
derechos aumenta al aumentar la edad de jubilación.
• Se
eligen los parámetros de tal manera
de minimizar los desvíos de las tasas de reemplazo resultantes
respecto a las tasas actuarialmente justas.
Formalmente:
1)
Jub C = TR(e, s).SBJ (8)
donde e representa la edad de jubilación, s es el número de períodos de servicio y SBJ es el salario básico jubilatorio.
2)
(9)
donde e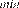 y s
y s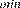 son las edades y períodos de servicio mínimos para acceder a la jubilación contributiva de beneficios
definidos.
son las edades y períodos de servicio mínimos para acceder a la jubilación contributiva de beneficios
definidos.
3) 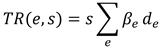 (10)
(10)
donde β > 0 es la tasa de adquisición de derechos
jubilatorios si la jubilación tiene lugar a la edad e y d
> 0 es la tasa de adquisición de derechos
jubilatorios si la jubilación tiene lugar a la edad e y d es una dummy que toma el valor 1 si la edad es e y 0 en
caso contrario.
es una dummy que toma el valor 1 si la edad es e y 0 en
caso contrario.
La ecuación (10) implica que TR(e, 0) = 0.
4)
Habrá que verificar empíricamente que se cumple:
TR(e,s) < TR(e',s) , sii e < e' (11)
O, lo que es lo mismo:
βe < βe' , sii e < e' (12)
 Gráficamente:
Gráficamente:
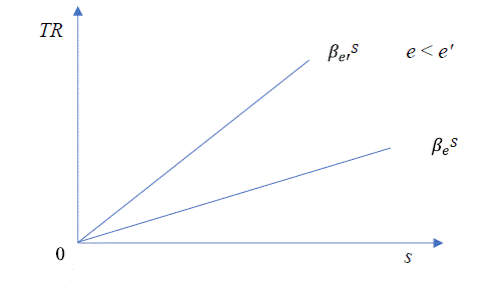
5) Para determinar las tasas de
adquisición de derechos jubilatorios propongo
ajustar la ecuación
(10) por MCO. De esta forma, minimizo los errores derivados de modelizar las tasas de
reemplazo con el modelo (10) en lugar de usar las TR actuarialmente justas[15]
 La estimación directa de (10) no permite
asegurar que se cumplirá (12). Si surgiera esta dificultad
en la estimación, una forma de asegurar el cumplimiento de esta propiedad es
elegir una estimación paramétrica apropiada. El caso más simple posible es
La estimación directa de (10) no permite
asegurar que se cumplirá (12). Si surgiera esta dificultad
en la estimación, una forma de asegurar el cumplimiento de esta propiedad es
elegir una estimación paramétrica apropiada. El caso más simple posible es
β = βe (13)
= βe (13)
Bajo la parametrización (13), sólo hay que determinar un parámetro, el parámetro β, y la condición (12) se cumplirá si y sólo si β
>0, lo cual puede
verificarse fácilmente después
de estimar. Obviamente que esta restricción va a
tener un costo en términos de deterioro del ajuste.
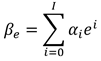 Se puede elegir una
forma paramétrica más flexible, como un polinomio, controlando que se siga
cumpliendo (12):
Se puede elegir una
forma paramétrica más flexible, como un polinomio, controlando que se siga
cumpliendo (12):
(14)
La ecuación (13) es un caso particular de (14), en el que α =α
=α =...=α
=...=α =0. Con la
formulación más flexible (14) hay que determinar los I+1 parámetros α
=0. Con la
formulación más flexible (14) hay que determinar los I+1 parámetros α . Es claro que
(14) es más flexible que (13), pero menos que
la formulación no paramétrica.
. Es claro que
(14) es más flexible que (13), pero menos que
la formulación no paramétrica.
Una vez ajustado el modelo, la medida más convencional de bondad de ajuste,
el R2, nos dará una medida
del error que estaremos cometiendo respecto a la equidad actuarial. El desvío
respecto a la equidad es 1-R2. Se me ocurren dos medidas más de bondad de
ajuste con mayor significado económico y de política social:
 Diferencia porcentual entre el gasto total del programa calculado
con(i) beneficios actuarialmente justos (cuentas nocionales) y (ii) el
programa BD.
Diferencia porcentual entre el gasto total del programa calculado
con(i) beneficios actuarialmente justos (cuentas nocionales) y (ii) el
programa BD.
 Distribución empírica de los desvíos de las jubilaciones BD y actuarialmente
justas. A partir de la distribución se pueden calcular indicadores
sintéticos de dispersión, como el rango intercuartílico y, más en
general, diversos intervalos de confianza.
Distribución empírica de los desvíos de las jubilaciones BD y actuarialmente
justas. A partir de la distribución se pueden calcular indicadores
sintéticos de dispersión, como el rango intercuartílico y, más en
general, diversos intervalos de confianza.
El primer indicador es de naturaleza macro y financiera. El
segundo apunta directamente a la equidad a nivel micro.
Estimaciones preliminares que realicé usando microdatos del BPS indican
que el ajuste es muy bueno. Es decir que las jubilaciones autofinanciadas por
un pilar de reparto pueden aproximarse muy bien con un esquema de adquisición
de derechos como el representado en la ecuación (10).
*Atento a ser un artículo por invitación, el presente trabajo no ha
sido sometido al habitual procedimiento evaluación externa por pares
**Este documento fue escrito en el marco del Plan anual de trabajo entre UNFPA
y la APFCS para 2021 y de los trabajos de la Comisión de Expertos en Seguridad
Social (CESS), creada en la ley 19.889, a fin de presentar un diagnóstico y
propuestas de reforma del sistema previsional uruguayo. Versiones preliminares
de este informe fueron discutidas en la comisión. Agradezco los comentarios
recibidos, pero las opiniones contenidas en este documento son de mi entera
responsabilidad.
[1] Puse un
único valor del parámetro a por simplicidad. Canadá tiene al menos dos valores,
según tramos de ingreso.
[2] Notar que este IMAS no es exactamente igual al del modelo anterior.
Uso el mismo nombre porque conceptualmente apuntan a lo mismo, pero están
definidos en forma un poco diferente. En el modelo anterior, IMAS es la máxima
jubilación con subsidio y aquí es el máximo ingreso total (jubilación más otros
ingresos) con subsidio.
[3] Estas estimaciones son muy preliminares: simplemente supuse que el
ingreso promedio a lo largo de la vida de los individuos es igual al ingreso corriente
informado en la ECH. Esto claramente no tiene en cuenta el ciclo de vida
reflejado en la curva de movilidad salarial. La densidad promedio de 60%, que
es una determinante clave de la TR financiable, podría ser razonable dadas las
estimaciones disponibles, pero el promedio es poco representativo de la
distribución en este caso. Para estimar el número de personas que quedan por
debajo de un umbral importa toda la distribución de las densidades, no alcanza
con conocer el promedio. En cualquier caso, es probable que la TR de 25%
supuesta para estos cálculos sea bastante representativa de lo que puede
financiarse en un sistema de reparto en Uruguay.
[4] Bene (2021) presenta una estimación usando supuestos algo diferentes
que arrojan densidades de cotización algo mayores. Discute brevemente algunos
desafíos de estas estimaciones.
[5] Ante las lagunas que existen en los registros de la historia laboral
antes de abril de 1996, el BPS re- conoce períodos de aportación para los que
no existe prueba documental en base a declaraciones de (i) testigos y (ii) del
interesado. El llamado “comunicado 42” es una resolución del directorio del BPS
de 2006 que reconoce años de servicio en base al testimonio del interesado.
[6] Para este cálculo,
supuse que el subsidio promedio que reciben los contribuyentes de la generación
1956 presentada en la sección 4.2 de este informe es representativo del
subsidio que habría que pagar a todas las personas de 65 años y más del país si
el pilar 0 fuera universal. Naturalmente, este es un supuesto simplificador
extremo y debe tomarse con cautela. Entiendo que sobreestima el costo porque,
como indiqué más arriba, no desconté otros ingresos que pudiera recibir la
persona. La secretaría técnica de la CESS ha realizado estimaciones mucho más
afinadas que las que presento aquí y, como cabía esperar, estiman un costo
sensiblemente menor al 2,4% del PBI que obtengo con mi estimación aproximada.
[7] “Your employment history is not a factor in determining eligibility.
You can receive the Old Age Security (OAS) pension even if you have never
worked or are still working.” (https://www.canada.ca/en/services/benefits/publicpensions/cpp/old-age-security/eligibility.html,
consultado el 26 de julio de 2021).
[8] “The guarantee pension is part of the national public pension that you
receive if you have had little or no pensionable income during your life. (…)
You may be entitled to a guarantee pension if you have reached the age of 65
and have a low or no income-based pension.”
[9] Obtenido en
https://www.aafp.cl/los-beneficios-del-pilar-solidario,consultado el 26 de
julio de 2021
[10] La jubilación “vieja” está entre comillada porque puede no corresponder
a la jubilación en el viejo régimen. Más abajo, en la ecuación (7) y texto
siguiente me refiero a este punto
[11] La ecuación (6) es un caso particular de la función logística general
a.(1+me-t'/τ))/(1+ne-t'/τ ), donde a = 1, m = 0,τ = 1 y t'= ln(t). Por el
momento, creo que este caso particular es suficiente para lo que necesito
hacer. Después, si fuera necesario, se podría explorar el caso general.
[12] El parámetro n mide el tiempo que lleva alcanzar la misma ponderación
de los regímenes viejo y nuevo de acuerdo a la curva logística: t(γ =0,5) = n.
[13] Este es un tipo de formulación que se observa en varios países
anglosajones. Lo que aquí llamo “tasa de adquisición de derechos” es lo que en
esa tradición se conoce como “accrual rate”. Una definición es: “The rate at
which pension benefit is built up as pensionable service in a defined benefit
scheme. Often expressed as a fraction or percentage of pensionable salary,
e.g., 1/60th (or 1.67 percent) for each year of service. Over 36 years, a 1.33
percent formula produces a pension of 48 percent of final average earnings.”
(https://theonn.ca/wp-content/uploads/2018/09/GLOS- SARY-OF-TERMS-PENSIONS.pdf,
acceso 10/05/2021).
[14] Esta formulación implica una subfamilia dentro de los diseños BD que
impone una restricción adicional: la ecuación lineal (10) tiene intercepto 0.
Esta restricción inevitablemente reduce la calidad del ajuste. La magnitud de
esa reducción es una cuestión empírica que habrá que estudiar con los datos.
Existen formulaciones basadas en la accrual rate más complejas que no imponen
esta restricción. Es el caso, por ejemplo de las fórmulas que usa la SSA de
EEUU.
[15] Recordar que, con el fin de poder formular el sistema BD en el formato
de tasa de adquisición de derechos por períodos de aporte, esta estimación debe
hacerse imponiendo intercepto 0. Esta opción está disponible en cualquier
paquete estadístico.
 Revista de Economía
y Estadística | Vol.LXI | N°1 | 2023 | pp. 11-42 | ISSN 0034-8066 | e-ISSN
2451-7321
Revista de Economía
y Estadística | Vol.LXI | N°1 | 2023 | pp. 11-42 | ISSN 0034-8066 | e-ISSN
2451-7321 ![]() Esta
obra está bajo una Licencia Creative Commons
Atribución-No Comercial-Sin Derivar 4.0 Internacional
Esta
obra está bajo una Licencia Creative Commons
Atribución-No Comercial-Sin Derivar 4.0 Internacional